Herhaalde metingen: Difference between revisions

From Wikistatistiek
Jump to navigation Jump to search
m (broken link verwijderd)
 
(42 intermediate revisions by 4 users not shown)
Line 1: Line 1:
{{auteurs|
{{auteurs|
|mainauthor= [[user:Nan van Geloven|ir. N van Geloven]]
|mainauthor= [[user:Nan van Geloven|dr. ir. N van Geloven]]
|coauthor=  prof. dr. A.H. Zwinderman
|coauthor=  prof. dr. A.H. Zwinderman
}}
}}
==Wat zijn herhaalde metingen?==
==Wat wordt bedoeld met herhaalde metingen?==


Herhaalde metingen zijn meerdere metingen van dezelfde variabele bij dezelfde persoon/patient, proefdier, of algemeen geformuleerd, dezelfde observationele eenheid. Voorbeelden:
Herhaalde metingen zijn meerdere metingen van dezelfde variabele bij dezelfde persoon, patiënt, proefdier, of algemeen geformuleerd, dezelfde observationele eenheid. Voorbeelden:


*'''herhaling in de tijd''': als patienten herhaaldelijk in een follow-up periode worden gemeten (of: voor en na een behandeling);
*'''herhaling in de tijd''': als dezelfde meting herhaaldelijk bij een patiënt wordt uitgevoerd, bijvoorbeeld  voor en na een behandeling, of gedurende een follow-up-periode;
*'''meerdere locaties''': metingen op meerdere locaties in het lichaam van dezelfde persoon (linker en rechter oog, meerdere coupes in een biopt, meerdere slices in een MRI beeld);
*'''meerdere locaties''': als metingen worden verricht op meerdere locaties in het lichaam van dezelfde persoon (linker- en rechteroog, meerdere coupes in een biopt, meerdere slices in een MRI beeld);
*'''meerdere condities''': als dezelfde patient onder twee of meer verschillende condities (bijv. behandelingen) wordt gemeten, bijvoorbeeld bij een cross-over studie;
*'''meerdere condities''': als dezelfde patiënt onder verschillende condities (bijv. twee behandelingen of testcondities) wordt gemeten, bijvoorbeeld bij een cross-over-studie of bij het vergelijken van beoordelaars;
*'''herhalingen tbv nauwkeurigheid''': als een meting een grote variatie binnen een persoon heeft (of een grote meetfout) dan kan het zinvol zijn om een aantal aparte metingen te doen;
*'''herhalingen ten bate van nauwkeurigheid''': als een meting een grote variatie binnen een persoon heeft (of een grote meetfout), of wanneer bijvoorbeeld de beperkte steekproefgrootte om een grotere nauwkeurigheid vraagt i.v.m. power, dan kan het zinvol zijn om een aantal aparte metingen te doen;
*'''multilevel structuren''': als metingen bij meerdere personen gedaan zijn die onderdeel uitmaken van dezelfde groep. Bijvoorbeeld patienten die dezelfde huisarts hebben, waarbij de interventie per huisartspraktijk is uitgevoerd. Het klassieke voorbeeld hier zijn leerlingen die dezelfde docent hebben en docenten die weer bij eenzelfde school horen.
*'''(andere) multilevel structuren''': als metingen bij meerdere personen gedaan zijn die onderdeel uitmaken van dezelfde groep, of waarvan anderszins kan worden verondersteld dat metingen van personen binnen hetzelfde cluster  meer op elkaar lijken dan twee metingen van personen uit een ander cluster. Bijvoorbeeld: Patiënten die dezelfde huisarts hebben (zeker indien de interventie per huisartspraktijk is uitgevoerd) of in hetzelfde ziekenhuis behandeld worden kunnen vaak niet als onafhankelijke observaties worden beschouwd. Het klassieke voorbeeld hier zijn leerlingen die dezelfde docent hebben en docenten die weer bij eenzelfde school horen.


==Waarom kun je bij herhaalde metingen geen standaard regressie model gebruiken?==
==Waarom kun je bij herhaalde metingen geen standaard regressiemodel gebruiken?==


Bij een standaard regressie model wordt aangenomen dat alle metingen onafhankelijk van elkaar zijn. Bij herhaalde metingen is het waarschijnlijk dat twee metingen van dezelfde persoon meer op elkaar lijken dan twee metingen van verschillende personen. Als dat zo is, dan zijn de metingen binnen dezelfde persoon niet onafhankelijk. Als bij herhaalde metingen geen rekening wordt gehouden met deze afhankelijkheid, dan zijn i.h.a. de standaard fouten en de p-waardes (onterecht!) te klein.  
Bij een standaard regressiemodel wordt aangenomen dat alle metingen onafhankelijk van elkaar zijn. Bij herhaalde metingen is het waarschijnlijk dat twee metingen van dezelfde persoon meer op elkaar lijken dan twee metingen van verschillende personen. Als dat zo is, dan zijn de metingen binnen dezelfde persoon niet onafhankelijk. Als bij herhaalde metingen geen rekening wordt gehouden met deze afhankelijkheid, dan zijn i.h.a. de standaardfouten en de p-waardes (onterecht!) te klein.  
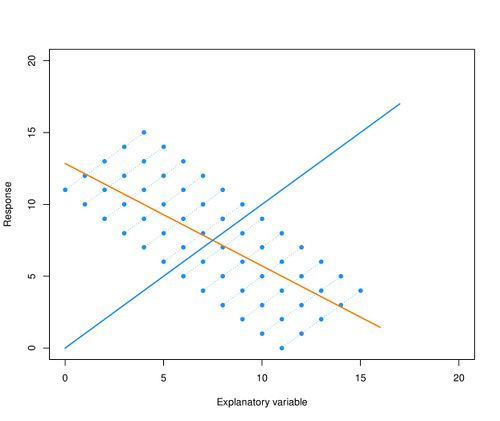
Bovendien kan de uitkomst van de regressie analyse volkomen fout zijn, zoals geillustreerd in het plaatje dat hieronder staat. In deze figuur worden de observaties van 6 personen getoond en elke persoon laat een duidelijk stijgende trend zien. Als de afhankelijkheid van de waarnemingen genegeerd wordt, dan is de best passende regressie lijn door de totale punten-wolk de gele dalende lijn en deze geeft geen correcte weergave van de trend per patient.
Bovendien kan de uitkomst van de regressie-analyse zelfs volkomen fout zijn, zoals geïllustreerd in het plaatje dat hieronder staat. In deze figuur worden de observaties van 12 personen getoond en elke persoon laat een duidelijk stijgende trend zien. Als de afhankelijkheid van de waarnemingen genegeerd wordt, dan is de best passende regressielijn door de totale puntenwolk de oranje dalende lijn en deze geeft geen correcte weergave van de trend per patiënt.


[[Image:Afbeelding herhaalde metingen.jpg]]
[[Image:14189829-0.jpg|500px]]


==Welke analyses zijn er mogelijk voor herhaalde metingen?==
==Welke analyses zijn er mogelijk voor herhaalde metingen?==


*'''Simpele methodes''': Soms kunnen herhaalde metingen samengevat worden in een enkele relevante maat. Je kunt bijvoorbeeld de meting van slechts een tijdpunt gebruiken, de verandering tussen twee meetpunten gebruiken, een samenvattende maat zoals het gemiddelde of de [[herhaalde metingen#area under the curve| area under the curve]] uitrekenen, of de tijd tot het bereiken van een bepaald level analyseren in een [[survival analyse]].
*'''Simpele methodes''': Soms kunnen herhaalde metingen samengevat worden in een enkele relevante maat. Je kunt bijvoorbeeld de meting van slechts een tijdpunt of de verandering tussen twee meetpunten gebruiken, een samenvattende maat zoals het gemiddelde of de [[herhaalde metingen#area under the curve| area under the curve]] uitrekenen, of de tijd tot het bereiken van een bepaalde grenswaarde van de uitkomstmaat te analyseren ([[survival analyse]]).
*'''Geavanceerde methodes''': Methodes die wel herhaalde metingen aankunnen zijn o.a. [[herhaalde metingen#mixed models|mixed models]], [[herhaalde metingen#repeated measurements ANOVA|repeated measurements ANOVA]] en Generalized Estimation Equations (GEE).  


De simpele methodes gebruiken maar een deel van de verzamelde informatie en dat levert vaak minder onderscheidingsvermogen (power) op.
De simpele methodes gebruiken maar een deel van de verzamelde informatie en dat levert vaak minder onderscheidingsvermogen (power) op. Daarentegen is de interpretatie ervan mogelijk veel intuïtiever dan bij het gebruiken van geavanceerdere methodes.  
Repeated measurements ANOVA is een specifieke variant van mixed-models, maar is alleen beschikbaar voor [[KEUZE TOETS#Van welk type is mijn data?|continue normaal verdeelde]] afhankelijke variabelen, die op vaste en dezelfde tijdstippen zijn gemeten in alle patienten.
Mixed-models en GEE-modellen zijn wat lastiger te specificeren, maar zijn flexibeler en zijn beschikbaar voor zowel continue normaal verdeelde afhankelijke variabelen, als voor bijv [[KEUZE TOETS#Van welk type is mijn data?|dichotome]] afhankelijke variabelen. Bovendien kunnen de mixed modellen ook omgaan met een zekere mate van [[missing values]], namelijk wanneer de data [[missing values#Welke soorten missing values zijn er?|missing at random]] zijn.


=area under the curve=
*'''Geavanceerde methodes''': Er bestaan ook methodes die wel alle herhaalde metingen gebruiken en corrigeren voor de afhankelijkheid van de metingen. Voorbeelden van analyses die geschikt zijn voor herhaalde metingen zijn o.a. [[mixed effects modellen]] (waaronder de [[repeated measures ANOVA]]) en [[Mixed effects modellen#Wat zijn GEE-modellen?| generalized estimating equations]] (GEE).


==Wat is een area under the curve en wanneer kun je die gebruiken?==
Repeated measurements ANOVA is een specifieke variant van mixed effects-modellen, specifiek voor [[KEUZE TOETS#Van welk type is mijn data?|continue normaal verdeelde]] afhankelijke variabelen die op vaste en dezelfde tijdstippen zijn gemeten in alle patiënten.  
Wanneer er op meerdere tijdstippen metingen zijn van een patient, kun je die samenvatten in een "area under the curve". Hierbij bereken je per patient de oppervlakte onder de gemeten punten in de tijd. Deze samenvattende maat gebruik je vervolgens voor de analyse.
Mixed effects-modellen en GEE-modellen zijn flexibeler dan de [[repeated measures ANOVA]] en zijn beschikbaar voor zowel continue normaal verdeelde afhankelijke variabelen, als voor bijvoorbeeld [[KEUZE TOETS#Van welk type is mijn data?|dichotome]] afhankelijke variabelen. Bovendien kunnen de mixed effects modellen, in tegenstelling tot de [[repeated measures ANOVA]] ook omgaan met een zekere mate van [[missing values]], namelijk wanneer de data [[missing values#Welke soorten missing values zijn er?|missing at random]] zijn.


==Hoe bereken ik met SPSS een area under the curve bij herhaalde metingen?==
==Hoe bereken ik met SPSS handig een area under the curve bij veel herhaalde metingen?==
''Ik wil graag van een bepaalde meting in de tijd, op verschillende tijdstippen gemeten, de 'area under the curve' bepalen. Ik kom er met SPSS niet uit. Ik moet er nl een stuk of 300 bepalen... heeft u nog een advies?
''Ik wil graag van een bepaalde meting in de tijd, op verschillende tijdstippen gemeten, de 'area under the curve' bepalen. Ik kom er met SPSS niet uit. Ik moet er namelijk een stuk of 300 bepalen... heeft u nog een advies?


Je kunt de volgende [[Media: Syntax_for_calculating_AUC.doc | syntax ]] gebruiken, deze rekent per patient een area under the curve uit. Bovenaan het document staat beschreven hoe je de variabelen in SPSS moet hebben staan.
Binnen SPSS kun je 'loops' gebruiken om bewerkingen of hercoderingen efficiënt uit te voeren. Je kunt de volgende [[Media: Syntax_for_calculating_AUC.doc | syntax ]] gebruiken, deze rekent per patiënt een area under the curve uit. Bovenaan het document staat beschreven hoe je de variabelen in SPSS moet hebben staan.


=mixed models=
== Hoe kan ik data van 4 experimenten combineren? ==
Mixed models kunnen op meerdere manieren gespecificeerd worden. Het is zinvol om een onderscheid te maken tussen
#onderzoeken waarbij alle patienten op (min of meer) dezelfde tijdstippen (of onder dezelfde condities) herhaald worden gemeten, en
#onderzoeken waarin het aantal herhaalde metingen per patient en/of de tijdstippen en condities verschillen tussen patienten.


====Situatie 1: herhaalde metingen op dezelfde momenten====
''De experimenten die ik verricht, heb ik in 4 sessies opgesplitst, aangezien het niet behapbaar was alle samples in een keer te verwerken. Nu blijkt dat de vergelijkingsgroepen (verschillende diagnoses) binnen elke serie toch wel erg klein zijn en vraag ik me af of en hoe ik de data van de 4 series zou kunnen combineren.


Als alle patienten op dezelfde tijdstippen (onder dezelfde condities) zijn gemeten, kan het mixed-model gezien worden als een uitbreiding van een standaard [[lineaire regressie| lineair model]]. In formulevorm ziet de uitbreiding van het standaard model er als volgt uit:
Wat wel gebruikt wordt bij zulk soort settings is het toepassen van een factor-correctie. Zie ook de referentie naar de paper van Ruijter <cite>[Ruijter2006]</cite> onderaan op deze pagina. Je kunt ook binnen een statistisch model een correctie voor de 'clustering'  binnen sessies meenemen, bijvoorbeeld door een [[herhaalde metingen#mixed models|mixed]] model of [[repeated measures ANOVA]] te gebruiken. Je beschouwt de experimenten dan als 'herhaalde metingen' binnen een sessie.


<math>\begin{equation*}
Y_{i,t} & = & a + b \times X_{i,t} + \epsilon_{i,t} \\
\end{equation*}</math>


waarbij <math>Y_{i,t}</math> de meting van de <math>i^{de}</math> patient is op het <math>t^{de}</math> tijdstip (conditie); <math>X_{i,t}</math> is de meting van de covariaat op dat moment en <math>\epsilon_{i,t}</math> is de afstand (of: ''residu'') van de datapunten tot de [[lineaire regressie#Hoe werkt (enkelvoudige) lineaire regressie?|regressielijn]]. Bij een standaard [[lineaire regressie]] zijn al deze residuen onafhankelijk van elkaar, maar bij herhaalde metingen is dat niet per se het geval. Namelijk, als het eerste datapunt van een patient (ver) boven (of onder) de lijn ligt, is het goed voorstelbaar dat volgende datapunten van dezelfde persoon ook boven (of onder) de regressielijn zullen liggen. Anders geformuleerd: datapunten van dezelfde persoon lijken meer op elkaar dan op datapunten van andere personen.
Bij een mixed model wordt rekening gehouden met de [[correlatie|correlaties]] tussen de residuen van metingen bij dezelfde patient. Dit kan op verschillende manieren en moet door de gebruiker worden gespecificeerd. Veel voorkomende correlatiestructuren zijn:
*compound symmetry, waarbij aangenomen wordt dat de correlaties tussen alle residuen van dezelfde persoon gelijk zijn. De eerste en de tweede meting van een persoon hangen dus even sterk met elkaar samen als de eerste en de laatste meting van die persoon;
*unstructured, waarbij geen enkele aanname wordt gemaakt over de correlaties. Iedere correlatie tussen twee tijdspunten wordt los van de anderen bepaald;
Er zijn nog diverse andere opties en de beste keuze hangt af van het type onderzoek en het aantal herhaalde metingen. Er zijn statistische maten die je helpen bij het maken van de keuze. Vaak wordt hiervoor de Akaike Information Criterium (AIC) gebruikt. Dit is een maat voor hoe goed het gekozen model past bij de data. Hoe lager de AIC, hoe beter het model past.
Deze eerste soort uitbreiding van het standaard lineaire model wordt ook wel 'Generalized Least Squares Model' genoemd.
====Situatie 2: herhaalde metingen op verschillende momenten====
Als het aantal herhaalde metingen per patient en/of de tijdstippen (condities) waarop er gemeten wordt verschillen tussen patienten, ligt het voor de hand om het [[lineaire regressie|lineaire model]] op een andere wijze uit te breiden. In situatie 1 werd de correlatie tussen meetpunten op verschillende tijdstippen direct gemodelleerd. Als er niet op vaste tijdstippen gemeten wordt, is dit niet logisch. De afhankelijkheid van metingen bij eenzelfde patient kan ook gemodelleerd worden met zogenaamde random effects. Met random effects wordt een inschatting gemaakt van de afwijking die metingen van eenzelfde patient hebben ten opzichte van de regressielijn. Hierbij maakt het niet uit hoe vaak en op welke tijdstippen een patient gemeten is; al zijn metingen worden verondersteld een vaste afwijking van de 'gemiddelde' regressielijn te hebben. In formulevorm ziet dit er als volgt uit:
<math>\begin{equation*}
Y_{i,t} & = & (a+ \alpha_i) + (b+\beta_i) \times X_{i,t}  + \epsilon_{i,t} \\
\end{equation*}</math>
waarbij de nu toegevoegde <math>\alpha_i</math> en <math>\beta_i</math> de specifieke afwijkingen van patient <math>i</math>  t.o.v. de regressielijn voorstellen. De <math>\alpha_i</math> is de afwijking van de intercept van patient <math>i</math> ten opzichte van de gemiddelde [[lineaire regressie#Hoe werkt een (enkelvoudig) lineair model?|intercept]] <math>a</math>. De <math>\beta_i</math> is de afwijking van de [[lineaire regressie#Hoe werkt een (enkelvoudig) lineair model?|helling]] (''slope'') van patient <math>i</math> ten opzichte van de gemiddelde helling <math>b</math> van de regressielijn. De <math>\alpha's</math> en <math>\beta's</math> worden niet direct geschat, in plaats daarvan wordt verondersteld dat zij normaal verdeeld zijn met gemiddelde 0. De standaard deviaties van deze verdelingen worden geschat.
De specificaties van de random effects kunnen nog uitgebreid worden en de fit van het model wordt gekwantificeerd met bijvoorbeeld de AIC. Ook hier geldt: het model met de laagste AIC past het beste bij de data.
Deze tweede soort modellen wordt vaak aangeduid als 'Random Effect Models'.
== Waar vind ik linear mixed models in SPSS?==
Je vindt de linear mixed models in SPSS 16 onder Analyze->Mixed models->Linear. In [[statistische software#SPSS|SPSS 16]] is er alleen nog een mixed model beschikbaar voor continue (normaal verdeelde) uitkomsten. In andere pakketten zoals [[statistische software#R|R]] (package 'nlme' en package 'lme4'), Stata ([http://www.gllamm.org GLAMM]) en [[statistische software#SAS|SAS]] zijn er ook mixed modellen beschikbaar voor bijvoorbeeld dichotome uitkomstmaten.
Let op: om een mixed model in SPSS te kunnen draaien moeten de data onder elkaar gestructureerd staan, waarbij iedere meting op een rij staat en er meerdere rijen zijn die bij dezelfde patient horen. In deze [http://www.spss.ch/upload/1126184451_Linear%20Mixed%20Effects%20Modeling%20in%20SPSS.pdf SPSS handleiding] staat stap voor stap beschreven hoe data te restructureren is in het gewenste format voor mixed models. Dit [http://distdell4.ad.stat.tamu.edu/spss_1/restructure.html filmpje] laat ook zien hoe de data te 'restructuren'. Als er drie herhaalde metingen van drie patienten zijn, ziet het resultaat er bijvoorbeeld zo uit:
{| border ="1" style="width:450px" align="center" cellpadding="3"
! patientnummer!! metingnr !! meting
|-
|align="center"| 1
|align="center"| 1
|align="center"| 10
|-
|align="center"| 1
|align="center"| 2
|align="center"| 9
|-
|align="center"| 1
|align="center"| 3
|align="center"| 11
|-
|align="center"| 2
|align="center"| 1
|align="center"| 8
|-
|align="center"| 2
|align="center"| 2
|align="center"| 11
|-
|align="center"| 2
|align="center"| 3
|align="center"| 12
|-
|align="center"| 3
|align="center"| 1
|align="center"| 5
|-
|align="center"| 3
|align="center"| 2
|align="center"| 8
|-
|align="center"| 3
|align="center"| 3
|align="center"| 9
|-
|}
De hierboven beschreven 'situatie 1' modellering gebeurt in SPSS middels het specificeren van de 'Repeated' (+bijbehorende repeated covariance type) in het eerste panel van de mixed procedure. De in 'situatie 2' besproken modellering wordt gespecificeerd onder de 'Random...' knop (let op: random intercept staat by default uit, bij covariance type kan correlatie tussen de random effects gespecificeerd worden). Vaak is het gebruik van 1 van beide opties (danwel repeated danwel random) voldoende om de correlatie in de data op te vangen. Gebruik maken van beide opties kan wel, maar zal soms leiden tot overbodige parameters.
==Voorbeeld: hoe analyseer ik met een mixed model een effect in de tijd?==
''Ik onderzoek een groep patienten die een operatie hebben ondergaan. We zijn geinteresseerd in de pijnscore (VAS) op verschillende tijdsmomenten na de operatie. De verwachting is (uiteraard) dat de pijn direct na de operatie heviger is dan bijv. 3 mnd daarna (dit klopt ook als je de data in een barplot zet). In eerste instantie heb ik de ANOVA for repeated measures gebruikt om te analyseren of de pijn significant verandert in de tijd. Maar, omdat ik een aantal missing data heb, heb ik ook geprobeerd een mixed models analyse (hier mijn [[Media:voorbeeld_mixed_model_spss.doc|syntax]]) te doen. Mijn vragen hierover: 
''1. Heb ik de juiste covariance structure gebruikt? (nl. AR1)
''2. Ik heb 'tijd' als fixed effect genomen omdat de afname van de VAS op specifieke tijdsmomenten gebeurde, klopt dat?
''3. Hoe geef de resultaten van deze mixed analyse weer?
1. Of AR(1) de beste is is niet zo te zeggen, dat hangt af van de correlatie tussen de tijdsmomenten in jouw data. Je kunt bijvoorbeeld alle mogelijke structuren draaien en dan degene met de kleinste AIC te kiezen (smaller is better zoals er ook onder staat).
2. Tijd is hier inderdaad een fixed variable, want je wilt hier de hypothese toetsen of er een verandering in de tijd is.
3. In de output vind je onder "fixed effects" een B die aangeeft wat het effect is per tijdspunt (tov het startpunt) en een bijbehorende p-waarde. Dit is de toets die je waarschijnlijk wilt rapporteren. Onder het kopje "mean estimates" vind je de schatting van het model voor de gemiddelde VAS waarde op ieder tijdpunt. Deze mean estimates zijn voor een lezer makkelijker te interpreteren dan de B's.
=repeated measurements ANOVA=
Repeated measurements ANOVA is een wat oudere term voor speciale vormen van mixed-models voor het analyseren van herhaalde metingen van een kwantitatieve afhankelijke variabele die normaal verdeeld is. Binnen het SPSS pakket wordt deze techniek aangeduid als GLM - repeated. Zoals eerder opgemerkt is deze procedure specifieke variant van mixed-models, maar is alleen beschikbaar voor continue normaal verdeelde afhankelijke variabelen, die op vaste en dezelfde tijdstippen zijn gemeten in alle patiënten.
Repeated measures ANOVA zoals in SPSS geimplementeerd, geeft twee soorten analyses, namelijk onder de aanname dat de correlaties tussen de herhaalde metingen allemaal dezelfde waarde hebben (compound symmetry) of zonder aannames over de correlaties (unstructured). In de SPSS output worden de compound-symmetry resultaten onder het kopje Tests of Within-Subjects Effects gerapporteerd en de unstructured resultaten onder het kopje Multivariate Tests. Wel handig is dat Mauchly's Test of Sphericity wordt gegeven; dat is een statistische toets van de nulhypothese dat de compound symmetry aanname klopt (kleine p-waardes van deze test zijn een indicatie dat compound symmetry niet goed past bij de data). Als sphericity (i.e. compound symmetry) wordt verworpen, dan kunnen ofwel de multivariate toets resultaten gebruikt worden, ofwel een Greenhouse-Geisser of een Huynh-Feldt correctie worden toegepast op de Tests of Within-Subjects Effects.
==Wanneer kan ik een repeated measurements ANOVA gebruiken?==
Je kunt een repeated measurements ANOVA gebruiken als:
* de afhankelijke variabele continue is en (per level van de onafhankelijke voorspeller) normaal verdeeld is,
* de herhaalde metingen op vaste tijdstippen in alle patienten zijn gedaan,
* er geen missende waardes zijn.
== Waar vind ik de repeated measurements ANOVA in SPSS?==
Je vindt de repeated measurements ANOVA in SPSS 16 onder Analyze->General Linear Model->Repeated measures.
Er geldt voor de repeated measurements ANOVA dat de herhaalde metingen van de patienten in aparte kolommen naast elkaar in de SPSS file moeten staan. Stel dat er drie herhaalde metingen van drie patienten zijn, dan ziet de data file er als volgt uit met vier kolommen:
{| border ="1" style="width:450px" align="center" cellpadding="3"
! patientnummer!! meting1 !! meting2 !! meting3
|-
|align="center"| 1
|align="center"| 10
|align="center"| 9
|align="center"| 11
|-
|align="center"| 2
|align="center"| 8
|align="center"| 11
|align="center"| 12
|-
|align="center"| 3
|align="center"| 5
|align="center"| 8
|align="center"| 9
|-
|}


= Referenties =
= Referenties =
<biblio>
#Gueorguieva2004 pmid=14993119
#West2009 pmid=19679634
#Ruijter2006 pmid=16398936
</biblio>


*[http://faculty.chass.ncsu.edu/garson/PA765/glmrepeated.htm Statnotes GLM Repeated measures] - zeer uitgebreide uitleg over de SPSS specificatie van een repeated measures ANOVA (engelstalig)
=Aanvullende bronnen=
*[http://faculty.chass.ncsu.edu/garson/PA765/multilevel.htm Statnotes Mixed Models] - zeer uitgebreide uitleg over mixed models en uitgebreide behandeling van wanneer voor mixed en wanneer voor GLM te kiezen (engelstalig)
*Deze post van Jonathan Bartlett over [http://thestatsgeek.com/2017/05/11/odds-ratios-collapsibility-marginal-vs-conditional-gee-vs-glmms/ Odds ratios, collapsibility, marginal vs. conditional, GEE vs GLMMs ] geeft aan wat het verschil is tussen GEE en GLMM (mixed model) aanpak bij binaire uitkomsten.
*[http://archpsyc.ama-assn.org/cgi/reprint/61/3/310 Move Over ANOVA: Progress in Analyzing Repeated-Measures Data and Its Reflection in Papers Published in the Archives of General Psychiatry. Gueorguieva R, Krystal JH. Arch Gen Psychiatry. 2004 Mar;61(3):310-7.]
* [http://www.theanalysisfactor.com/repeated-and-random-2/ The analysis factor - The Repeated and Random Statements in Mixed Models for Repeated Measures] info over het onderscheid tussen de repeated en de random statement in SPSS mixed.
*[http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pubmed&pubmedid=16398936 Ruijter JM, Thygesen HH, Schoneveld OJ, Das AT, Berkhout B, Lamers WH, Factor correction as a tool to eliminate between-session variation in replicate experiments: application to molecular biology and retrovirology, Retrovirology. 2006 Jan 6;3:2]
* [http://www.theanalysisfactor.com/repeated-measures-approaches/ The analysis factor] info over de verschillende aanpakken voor herhaalde metingen: repeated measurements anova, marginal model, mixed model.
* [http://www.floppybunny.org/robin/web/virtualclassroom/stats/course2.html Robin Beaumont Heath Informatics course material] Vrij te gebruiken cursusmateriaal over linear mixed models met uileg van specificatie in zowel SPSS als R, zie week 6 7 en 8. Inclusief bijbehorende Youtube instructiefilmpjes.


Sofwaretips:
=Sofwaretips=
*[http://www.gllamm.org/ GLLAMM] Een familie functies (vrij te downloaden/attachen) in [[Statistische software#Stata|Stata]], waarbij er opties zijn voor het modelleren van herhaaldelijk gemeten niet continue uitkomstmaten (dichotome, ordinale etc).
*[http://www.gllamm.org/ GLLAMM] Een familie functies (vrij te downloaden/attachen) in [[Statistische software#Stata|Stata]], waarbij er opties zijn voor het modelleren van herhaaldelijk gemeten niet continue uitkomstmaten (dichotome, ordinale etc).
*[http://tigger.uic.edu/~hedeker/mix.html SuperMix] Een standalone programma geschikt voor het modelleren van herhaaldelijk gemeten niet continue uitkomstmaten (dichotome, ordinale etc).
*[http://tigger.uic.edu/~hedeker/mix.html SuperMix] Een standalone programma geschikt voor het modelleren van herhaaldelijk gemeten niet continue uitkomstmaten (dichotome, ordinale etc).


 
{{onderschrift}}
<div style="background-color:#e8f1ff; margin:0.5em; padding:1em; border:1px solid #C8D0DC;">
Terug naar [[OVERZICHT]] voor een overzicht van alle statistische onderwerpen op deze wiki.
 
Terug naar [[KEUZE TOETS]] voor hulp bij het uitzoeken van een geschikte toets of analyse.
<div>

Latest revision as of 16:11, 20 November 2024

Auteur dr. ir. N van Geloven
Co-Auteur prof. dr. A.H. Zwinderman
auteurschap op deze site

Wat wordt bedoeld met herhaalde metingen?

Herhaalde metingen zijn meerdere metingen van dezelfde variabele bij dezelfde persoon, patiënt, proefdier, of algemeen geformuleerd, dezelfde observationele eenheid. Voorbeelden:

  • herhaling in de tijd: als dezelfde meting herhaaldelijk bij een patiënt wordt uitgevoerd, bijvoorbeeld voor en na een behandeling, of gedurende een follow-up-periode;
  • meerdere locaties: als metingen worden verricht op meerdere locaties in het lichaam van dezelfde persoon (linker- en rechteroog, meerdere coupes in een biopt, meerdere slices in een MRI beeld);
  • meerdere condities: als dezelfde patiënt onder verschillende condities (bijv. twee behandelingen of testcondities) wordt gemeten, bijvoorbeeld bij een cross-over-studie of bij het vergelijken van beoordelaars;
  • herhalingen ten bate van nauwkeurigheid: als een meting een grote variatie binnen een persoon heeft (of een grote meetfout), of wanneer bijvoorbeeld de beperkte steekproefgrootte om een grotere nauwkeurigheid vraagt i.v.m. power, dan kan het zinvol zijn om een aantal aparte metingen te doen;
  • (andere) multilevel structuren: als metingen bij meerdere personen gedaan zijn die onderdeel uitmaken van dezelfde groep, of waarvan anderszins kan worden verondersteld dat metingen van personen binnen hetzelfde cluster meer op elkaar lijken dan twee metingen van personen uit een ander cluster. Bijvoorbeeld: Patiënten die dezelfde huisarts hebben (zeker indien de interventie per huisartspraktijk is uitgevoerd) of in hetzelfde ziekenhuis behandeld worden kunnen vaak niet als onafhankelijke observaties worden beschouwd. Het klassieke voorbeeld hier zijn leerlingen die dezelfde docent hebben en docenten die weer bij eenzelfde school horen.

Waarom kun je bij herhaalde metingen geen standaard regressiemodel gebruiken?

Bij een standaard regressiemodel wordt aangenomen dat alle metingen onafhankelijk van elkaar zijn. Bij herhaalde metingen is het waarschijnlijk dat twee metingen van dezelfde persoon meer op elkaar lijken dan twee metingen van verschillende personen. Als dat zo is, dan zijn de metingen binnen dezelfde persoon niet onafhankelijk. Als bij herhaalde metingen geen rekening wordt gehouden met deze afhankelijkheid, dan zijn i.h.a. de standaardfouten en de p-waardes (onterecht!) te klein. Bovendien kan de uitkomst van de regressie-analyse zelfs volkomen fout zijn, zoals geïllustreerd in het plaatje dat hieronder staat. In deze figuur worden de observaties van 12 personen getoond en elke persoon laat een duidelijk stijgende trend zien. Als de afhankelijkheid van de waarnemingen genegeerd wordt, dan is de best passende regressielijn door de totale puntenwolk de oranje dalende lijn en deze geeft geen correcte weergave van de trend per patiënt.

14189829-0.jpg

Welke analyses zijn er mogelijk voor herhaalde metingen?

  • Simpele methodes: Soms kunnen herhaalde metingen samengevat worden in een enkele relevante maat. Je kunt bijvoorbeeld de meting van slechts een tijdpunt of de verandering tussen twee meetpunten gebruiken, een samenvattende maat zoals het gemiddelde of de area under the curve uitrekenen, of de tijd tot het bereiken van een bepaalde grenswaarde van de uitkomstmaat te analyseren (survival analyse).

De simpele methodes gebruiken maar een deel van de verzamelde informatie en dat levert vaak minder onderscheidingsvermogen (power) op. Daarentegen is de interpretatie ervan mogelijk veel intuïtiever dan bij het gebruiken van geavanceerdere methodes.

Repeated measurements ANOVA is een specifieke variant van mixed effects-modellen, specifiek voor continue normaal verdeelde afhankelijke variabelen die op vaste en dezelfde tijdstippen zijn gemeten in alle patiënten. Mixed effects-modellen en GEE-modellen zijn flexibeler dan de repeated measures ANOVA en zijn beschikbaar voor zowel continue normaal verdeelde afhankelijke variabelen, als voor bijvoorbeeld dichotome afhankelijke variabelen. Bovendien kunnen de mixed effects modellen, in tegenstelling tot de repeated measures ANOVA ook omgaan met een zekere mate van missing values, namelijk wanneer de data missing at random zijn.

Hoe bereken ik met SPSS handig een area under the curve bij veel herhaalde metingen?

Ik wil graag van een bepaalde meting in de tijd, op verschillende tijdstippen gemeten, de 'area under the curve' bepalen. Ik kom er met SPSS niet uit. Ik moet er namelijk een stuk of 300 bepalen... heeft u nog een advies?

Binnen SPSS kun je 'loops' gebruiken om bewerkingen of hercoderingen efficiënt uit te voeren. Je kunt de volgende syntax gebruiken, deze rekent per patiënt een area under the curve uit. Bovenaan het document staat beschreven hoe je de variabelen in SPSS moet hebben staan.

Hoe kan ik data van 4 experimenten combineren?

De experimenten die ik verricht, heb ik in 4 sessies opgesplitst, aangezien het niet behapbaar was alle samples in een keer te verwerken. Nu blijkt dat de vergelijkingsgroepen (verschillende diagnoses) binnen elke serie toch wel erg klein zijn en vraag ik me af of en hoe ik de data van de 4 series zou kunnen combineren.

Wat wel gebruikt wordt bij zulk soort settings is het toepassen van een factor-correctie. Zie ook de referentie naar de paper van Ruijter [1] onderaan op deze pagina. Je kunt ook binnen een statistisch model een correctie voor de 'clustering' binnen sessies meenemen, bijvoorbeeld door een mixed model of repeated measures ANOVA te gebruiken. Je beschouwt de experimenten dan als 'herhaalde metingen' binnen een sessie.


Referenties

  1. Ruijter JM, Thygesen HH, Schoneveld OJ, Das AT, Berkhout B, and Lamers WH. Factor correction as a tool to eliminate between-session variation in replicate experiments: application to molecular biology and retrovirology. Retrovirology. 2006 Jan 6;3:2. DOI:10.1186/1742-4690-3-2 | PubMed ID:16398936 | HubMed [Ruijter2006]
  2. Gueorguieva R and Krystal JH. Move over ANOVA: progress in analyzing repeated-measures data and its reflection in papers published in the Archives of General Psychiatry. Arch Gen Psychiatry. 2004 Mar;61(3):310-7. DOI:10.1001/archpsyc.61.3.310 | PubMed ID:14993119 | HubMed [Gueorguieva2004]
  3. West BT. Analyzing longitudinal data with the linear mixed models procedure in SPSS. Eval Health Prof. 2009 Sep;32(3):207-28. DOI:10.1177/0163278709338554 | PubMed ID:19679634 | HubMed [West2009]

All Medline abstracts: PubMed | HubMed

Aanvullende bronnen

Sofwaretips

  • GLLAMM Een familie functies (vrij te downloaden/attachen) in Stata, waarbij er opties zijn voor het modelleren van herhaaldelijk gemeten niet continue uitkomstmaten (dichotome, ordinale etc).
  • SuperMix Een standalone programma geschikt voor het modelleren van herhaaldelijk gemeten niet continue uitkomstmaten (dichotome, ordinale etc).

Klaar met lezen? Je kunt naar het OVERZICHT van alle statistische onderwerpen op deze wiki gaan of naar de pagina KEUZE TOETS voor hulp bij het uitzoeken van een geschikte toets of analyse. Wil je meer leren over biostatistiek? Volg dan de AMC e-learning Practical Biostatistics. Vind je op deze pagina's iets dat niet klopt? Werkt een link niet? Of wil je bijdragen aan de wiki? Neem dan contact met ons op.

De wiki biostatistiek is een initiatief van de voormalige helpdesk statistiek van Amsterdam UMC, locatie AMC. Medewerkers van Amsterdam UMC kunnen via intranet ondersteuning aanvragen.

Retrieved from "https://wikibiostatistiek.amsterdamumc.org/index.php?title=Herhaalde_metingen&oldid=3722"