One-way ANOVA: Difference between revisions
No edit summary |
|||
| (12 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
De One-way ANOVA (voluit One-way ANalysis Of VAriance) is een parametrische toetsings procedure voor het testen van hypothesen over de gemiddelden van (semi-)continue data. De ANOVA toetst of de gemiddelden van 2 of meer onafhankelijke groepen | {{auteurs| | ||
|mainauthor= [[user:Nan van Geloven|dr. ir. N. van Geloven]] | |||
|coauthor= | |||
}} | |||
De One-way ANOVA (voluit One-way ANalysis Of VAriance) is een parametrische toetsings procedure voor het testen van hypothesen over de gemiddelden van (semi-)continue data. De ANOVA toetst of de gemiddelden van 2 of meer onafhankelijke groepen gelijk zijn. | |||
== Wanneer gebruik ik de One-way ANOVA? == | == Wanneer gebruik ik de One-way ANOVA? == | ||
| Line 5: | Line 9: | ||
Als je wilt toetsen of de gemiddelden van 2 of meer groepen aan elkaar gelijk zijn, kun je de ongepaarde One-way ANOVA gebruiken. In de regel wordt de One-way ANOVA alleen gebruikt bij het vergelijken van minstens 3 groepen. Voor de vergelijking van twee groepen is de One-way ANOVA gelijk aan het uitvoeren van een [[t-toets#ongepaarde t-toets | ongepaarde t-toets]]. | Als je wilt toetsen of de gemiddelden van 2 of meer groepen aan elkaar gelijk zijn, kun je de ongepaarde One-way ANOVA gebruiken. In de regel wordt de One-way ANOVA alleen gebruikt bij het vergelijken van minstens 3 groepen. Voor de vergelijking van twee groepen is de One-way ANOVA gelijk aan het uitvoeren van een [[t-toets#ongepaarde t-toets | ongepaarde t-toets]]. | ||
De One-way ANOVA veronderstelt dat het de drie groepen uit een multivariate normale verdeling afkomstig zijn (in iedere groep heeft de variabele een normale verdeling). Er wordt vervolgens getoetst of de gemiddelden van deze verdelingen gelijk zijn of niet. De One-way ANOVA veronderstelt daarnaast dat de groepen uit een verdeling komen met dezelfde variantie (spreiding). Met bijvoorbeeld 'Levene's Test for equality of variance' kun je testen of de variantie in de groepen gelijk verondersteld kan worden. Indien niet aan deze voorwaarden voldaan is, kan een niet | De One-way ANOVA veronderstelt dat het de drie groepen uit een multivariate normale verdeling afkomstig zijn (in iedere groep heeft de variabele een normale verdeling). Er wordt vervolgens getoetst of de gemiddelden van deze verdelingen gelijk zijn of niet. De One-way ANOVA veronderstelt daarnaast dat de groepen uit een verdeling komen met dezelfde variantie (spreiding). Met bijvoorbeeld 'Levene's Test for equality of variance' kun je testen of de variantie in de groepen gelijk verondersteld kan worden. Indien niet aan deze voorwaarden voldaan is, kan een niet parametrische [[Kruskal Wallis]] analyse overwogen worden. | ||
Voorbeeld van het gebruik van de One-way ANOVA: | Voorbeeld van het gebruik van de One-way ANOVA: | ||
Stel je wilt testen of de (10 log) CD4 count gelijk is voor drie armen in een studie. | Stel je wilt testen of de (10 log) CD4 count gelijk is voor drie armen in een studie. | ||
{| border ="1" style=align="center" cellpadding="3" cellspacing="0" | {| border ="1" style=align="center" cellpadding="3" cellspacing="0" | ||
| Line 29: | Line 31: | ||
|colspan="5" rowspan="2"| *Variables are denoted as mean (SD). **Group differences were tested with one-way ANOVA. | |colspan="5" rowspan="2"| *Variables are denoted as mean (SD). **Group differences were tested with one-way ANOVA. | ||
|} | |} | ||
[[Image:figuur ANOVA0.jpg]] | |||
== Wat doe ik als mijn data niet voldoen aan de assumptie van gelijke varianties in de groepen? == | |||
''Wij hebben een dierexperimentele studie waarbij ratten met verschillende strategieen zijn beademend en al dan niet een medicamenteuze voorbehandeling hebben gekregen. In ieder van de 4 experimentele groepen zijn 6 ratten geincludeerd. Ik heb de one-way ANOVA gebruikt indien de test voor gelijke varianties (Bartlett's test for equal variances) geen significante waarde opleverde. Indien de p-waarde van deze test <0.05 was, heb ik een log transformatie op de data toegepast en de ANOVA analyse hierop gerund. Indien de p-waarde na transformatie nog steeds ruim onder de 0.05 was, heb ik de Kruskall-Wallis analyse gebruikt. Volgens de checklist die GraphPad Prism levert, zou dit statistisch verantwoord zijn. Over 1 analyse heb ik echter een vraag. De Bartlett's test geeft nl een waarde van p<0.0001 indien de data niet getransformeerd zijn en na log transformatie een waarde van 0.0318. Zowel de ANOVA als Kruskal-Wallis geeft een statistisch verschil aan tussen de verschillende experimentele groepen maar de post-hoc analyses verschillen behoorlijk, waarbij bij de non-parametrische test in de post-hoc analyse (Dunns test) nagenoeg geen verschillen tussen de groepen aangeeft. | |||
''Nu zegt de uitleg die bij het programma wordt geleverd, dat je kritisch moet kijken of je de ANOVA verwerpt indien de Bartlett's test niet veel onder de 0.05 uitkomt, aangezien bij kleine aantallen de Kruskall-Wallis niet zo'n krachtige test is. Kan ik dit inderdaad doen, want als ik naar de grafieken kijk, geeft de post-hoc analyse van de ANOVA (de Newman-Keuls test) een uitslag die veel meer bij de visuele data past? | |||
Je verhaal klopt. Testen voor gelijke varianties zijn soms streng (met name bij de kleine aantallen). Een p-waarde van 0.04 zit dicht bij je grens waarbij je het wel mag accepteren. Ik zou inderdaad naar de ruwe (log) waardes kijken en me afvragen wat je daar ziet. Bij kleine aantallen kunnen met name outliers zorgen voor andere resultaten. Je zou daar dus nog naar kunnen kijken. Als je inderdaad een enorme outlier hebt, zou je eens moeten kijken als die eruit is of je ANOVA van de ln waarde dan nog steeds significant is. | |||
Non-parametrisch is inderdaad vaak strenger (en dus minder snel significant) dan paramtetrisch, maar wordt ook veel minder door outliers beinvloed. | |||
== Waar vind ik de One-way ANOVA in SPSS?== | |||
Je vindt de One-way ANOVA in SPSS onder Analyze->Compare Means. | |||
== Referenties == | |||
*[http://www.teorekol.lu.se/statistics_for_biologists/SPSS_ANOVA_guide.pdf A short guide to running ANOVA:s in SPSS] Door Jörgen Ripa - legt uit hoe one-way anova's, maar ook meer geavanceerde ANOVAs, in SPSS gespecificeerd kunnen. Zeer handig om de ANOVA SPSS syntax beter te begrijpen. | |||
{{onderschrift}} | |||
Latest revision as of 12:53, 13 May 2024
| Auteur | dr. ir. N. van Geloven | |
| Co-Auteur | ||
| auteurschap op deze site | ||
De One-way ANOVA (voluit One-way ANalysis Of VAriance) is een parametrische toetsings procedure voor het testen van hypothesen over de gemiddelden van (semi-)continue data. De ANOVA toetst of de gemiddelden van 2 of meer onafhankelijke groepen gelijk zijn.
Wanneer gebruik ik de One-way ANOVA?
Als je wilt toetsen of de gemiddelden van 2 of meer groepen aan elkaar gelijk zijn, kun je de ongepaarde One-way ANOVA gebruiken. In de regel wordt de One-way ANOVA alleen gebruikt bij het vergelijken van minstens 3 groepen. Voor de vergelijking van twee groepen is de One-way ANOVA gelijk aan het uitvoeren van een ongepaarde t-toets.
De One-way ANOVA veronderstelt dat het de drie groepen uit een multivariate normale verdeling afkomstig zijn (in iedere groep heeft de variabele een normale verdeling). Er wordt vervolgens getoetst of de gemiddelden van deze verdelingen gelijk zijn of niet. De One-way ANOVA veronderstelt daarnaast dat de groepen uit een verdeling komen met dezelfde variantie (spreiding). Met bijvoorbeeld 'Levene's Test for equality of variance' kun je testen of de variantie in de groepen gelijk verondersteld kan worden. Indien niet aan deze voorwaarden voldaan is, kan een niet parametrische Kruskal Wallis analyse overwogen worden.
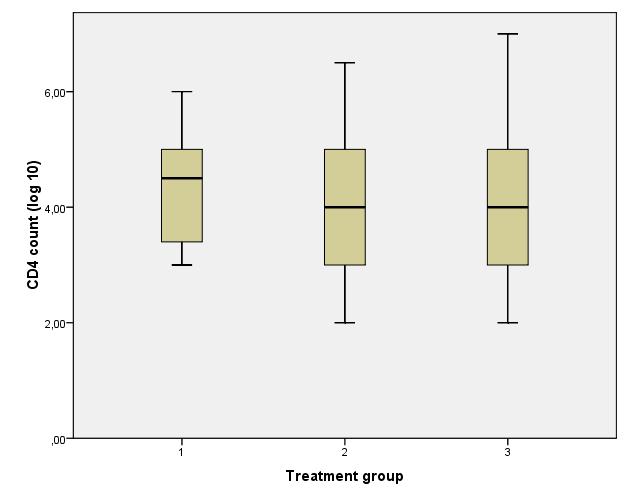
Voorbeeld van het gebruik van de One-way ANOVA: Stel je wilt testen of de (10 log) CD4 count gelijk is voor drie armen in een studie.
| Table 1. log 10 CD4 counts in the three treatment arms | ||||
|---|---|---|---|---|
| Variable* | Treatment arm 1 | Treatment arm 2 | Treatment arm 3 | p-value** |
| Log 10 CD4 counts | 4.5 (1.3) | 4.0 (1.5) | 4.1 (1.6) | 0.66 |
| *Variables are denoted as mean (SD). **Group differences were tested with one-way ANOVA. | ||||
Wat doe ik als mijn data niet voldoen aan de assumptie van gelijke varianties in de groepen?
Wij hebben een dierexperimentele studie waarbij ratten met verschillende strategieen zijn beademend en al dan niet een medicamenteuze voorbehandeling hebben gekregen. In ieder van de 4 experimentele groepen zijn 6 ratten geincludeerd. Ik heb de one-way ANOVA gebruikt indien de test voor gelijke varianties (Bartlett's test for equal variances) geen significante waarde opleverde. Indien de p-waarde van deze test <0.05 was, heb ik een log transformatie op de data toegepast en de ANOVA analyse hierop gerund. Indien de p-waarde na transformatie nog steeds ruim onder de 0.05 was, heb ik de Kruskall-Wallis analyse gebruikt. Volgens de checklist die GraphPad Prism levert, zou dit statistisch verantwoord zijn. Over 1 analyse heb ik echter een vraag. De Bartlett's test geeft nl een waarde van p<0.0001 indien de data niet getransformeerd zijn en na log transformatie een waarde van 0.0318. Zowel de ANOVA als Kruskal-Wallis geeft een statistisch verschil aan tussen de verschillende experimentele groepen maar de post-hoc analyses verschillen behoorlijk, waarbij bij de non-parametrische test in de post-hoc analyse (Dunns test) nagenoeg geen verschillen tussen de groepen aangeeft. Nu zegt de uitleg die bij het programma wordt geleverd, dat je kritisch moet kijken of je de ANOVA verwerpt indien de Bartlett's test niet veel onder de 0.05 uitkomt, aangezien bij kleine aantallen de Kruskall-Wallis niet zo'n krachtige test is. Kan ik dit inderdaad doen, want als ik naar de grafieken kijk, geeft de post-hoc analyse van de ANOVA (de Newman-Keuls test) een uitslag die veel meer bij de visuele data past?
Je verhaal klopt. Testen voor gelijke varianties zijn soms streng (met name bij de kleine aantallen). Een p-waarde van 0.04 zit dicht bij je grens waarbij je het wel mag accepteren. Ik zou inderdaad naar de ruwe (log) waardes kijken en me afvragen wat je daar ziet. Bij kleine aantallen kunnen met name outliers zorgen voor andere resultaten. Je zou daar dus nog naar kunnen kijken. Als je inderdaad een enorme outlier hebt, zou je eens moeten kijken als die eruit is of je ANOVA van de ln waarde dan nog steeds significant is. Non-parametrisch is inderdaad vaak strenger (en dus minder snel significant) dan paramtetrisch, maar wordt ook veel minder door outliers beinvloed.
Waar vind ik de One-way ANOVA in SPSS?
Je vindt de One-way ANOVA in SPSS onder Analyze->Compare Means.
Referenties
- A short guide to running ANOVA:s in SPSS Door Jörgen Ripa - legt uit hoe one-way anova's, maar ook meer geavanceerde ANOVAs, in SPSS gespecificeerd kunnen. Zeer handig om de ANOVA SPSS syntax beter te begrijpen.
Klaar met lezen? Je kunt naar het OVERZICHT van alle statistische onderwerpen op deze wiki gaan of naar de pagina KEUZE TOETS voor hulp bij het uitzoeken van een geschikte toets of analyse. Wil je meer leren over biostatistiek? Volg dan de AMC e-learning Practical Biostatistics. Vind je op deze pagina's iets dat niet klopt? Werkt een link niet? Of wil je bijdragen aan de wiki? Neem dan contact met ons op.
De wiki biostatistiek is een initiatief van de voormalige helpdesk statistiek van Amsterdam UMC, locatie AMC. Medewerkers van Amsterdam UMC kunnen via intranet ondersteuning aanvragen.