Lineaire regressie: Difference between revisions
J Wezelman (talk | contribs) |
|||
| Line 18: | Line 18: | ||
==Hoe werkt (enkelvoudige) lineaire regressie?== | ==Hoe werkt (enkelvoudige) lineaire regressie?== | ||
In lineaire regressie bepalen we de regressielijn, die het beste de lineaire relatie tussen de <math>X</math> en <math>Y</math> variabelen beschrijft. De lineaire regressielijn wordt geschat met behulp van de vergelijking: | In lineaire regressie bepalen we de regressielijn, die het beste de lineaire relatie tussen de <math>X</math> en <math>Y</math> variabelen beschrijft. De lineaire regressielijn wordt geschat met behulp van de vergelijking: | ||
<math>Y = a+b \times X + \epsilon</math> | |||
Y | |||
</math> | |||
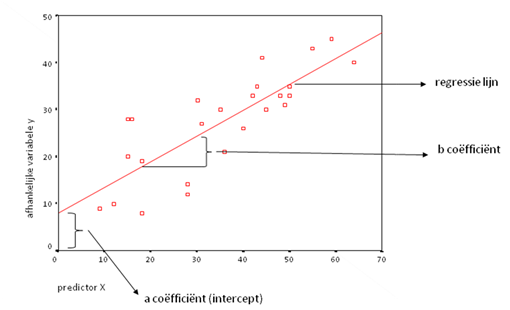
<math>Y</math> is de afhankelijke, uitkomstvariabele; <math>X</math> de onafhankelijke voorspeller; en 'a' en 'b' zijn de regressiecoëfficiënten; <math>\epsilon</math> representeert de afstand tussen de regressielijn en de datapunten (de residuen). Regressiecoëfficiënt ‘a’ wordt ook wel de intercept genoemd, en geeft de waarde van <math>Y</math> aan als <math>X=0</math> (de intercept bepaalt dus de hoogte van de regressielijn). De regressiecoëfficiënt ‘b’ weerspiegelt de helling (''slope'') van de regressielijn, en geeft de gemiddelde toename van <math>Y</math> aan als de <math>X</math> variabele met 1 eenheid toeneemt. | <math>Y</math> is de afhankelijke, uitkomstvariabele; <math>X</math> de onafhankelijke voorspeller; en 'a' en 'b' zijn de regressiecoëfficiënten; <math>\epsilon</math> representeert de afstand tussen de regressielijn en de datapunten (de residuen). Regressiecoëfficiënt ‘a’ wordt ook wel de intercept genoemd, en geeft de waarde van <math>Y</math> aan als <math>X=0</math> (de intercept bepaalt dus de hoogte van de regressielijn). De regressiecoëfficiënt ‘b’ weerspiegelt de helling (''slope'') van de regressielijn, en geeft de gemiddelde toename van <math>Y</math> aan als de <math>X</math> variabele met 1 eenheid toeneemt. | ||
Revision as of 09:52, 1 July 2015
| Auteur | prof dr R.J. de Haan | |
| Co-Auteur | ||
| auteurschap op deze site | ||
Wanneer gebruik ik een lineair regressie model?
Als je een correlatietechniek toepast, ben je geïnteresseerd in de mate van samenhang tussen twee variabelen en , bijvoorbeeld een onderzoek naar de samenhang tussen leeftijd en scores op een cognitieve test. Met lineaire regressie ga je een stap verder. Met deze techniek probeer je de waarden van de uitkomst via een lineair verband te voorspellen uit die van . De uitkomstvariabele wordt de afhankelijke variabele genoemd, en de voorspeller de onafhankelijke variabele. We spreken van enkelvoudige (ook wel simple of univariable) regressie als we de uitkomst willen voorspellen met één predictor. In de praktijk zal dat in vele gevallen niet voldoende zijn en is het wenselijk om de effecten van twee of meer voorspellers te analyseren. We spreken dan van meervoudige (ook wel multiple of multivariable) lineaire regressie.
Om een lineaire regressie te kunnen gebruiken, moeten de onderzoeksgegevens aan een aantal statistische voorwaarden voldoen:
- Over de gehele range van geobserveerde waarden moet sprake zijn van een lineaire samenhang tussen de onafhankelijke variabele en de afhankelijke variabele (tip: maak eerst een scatterplot om de aard van de samenhang tussen en te exploreren);
- Wat betreft het type data mogen de variabelen zowel discreet als continu zijn. De afhankelijke variabele mag alleen continu zijn;
- Voor elke waarde van moeten de observaties van onafhankelijk van elkaar zijn; dat wil zeggen dat de variabelen slechts 1 keer bij een persoon zijn gemeten. Lineaire regressie is dus niet geschikt om voor onderzoeksgegevens te analyseren waarbij de patiënten herhaaldelijk in de tijd zijn gemeten (voor herhaalde metingen bestaan andere technieken).
- De variabele heeft een normaal verdeling voor elke waarde van .
- De verdelingen van de variabele hebben een gelijke variantie (of standaard deviatie) voor elke waarde van .
De assumpties 1, 4 en 5 kunnen met behulp van de residuen van het lineaire model worden gecontroleerd.
Hoe werkt (enkelvoudige) lineaire regressie?
In lineaire regressie bepalen we de regressielijn, die het beste de lineaire relatie tussen de en variabelen beschrijft. De lineaire regressielijn wordt geschat met behulp van de vergelijking:
is de afhankelijke, uitkomstvariabele; de onafhankelijke voorspeller; en 'a' en 'b' zijn de regressiecoëfficiënten; representeert de afstand tussen de regressielijn en de datapunten (de residuen). Regressiecoëfficiënt ‘a’ wordt ook wel de intercept genoemd, en geeft de waarde van aan als (de intercept bepaalt dus de hoogte van de regressielijn). De regressiecoëfficiënt ‘b’ weerspiegelt de helling (slope) van de regressielijn, en geeft de gemiddelde toename van aan als de variabele met 1 eenheid toeneemt.
Hoe interpreteer ik mijn SPSS output bij gebruik van een enkelvoudig lineair model?
Stel dat we in een steekproef van n=25 de Pearson’s correlatie tussen de leeftijd van proefpersonen en hun lichaamsvetpercentage 0.81 is. We willen deze samenhang echter niet alleen beschrijven, maar op basis van de leeftijd van de persoon nu ook een voorspelling doen over zijn of haar lichaamsvetpercentage. Als we in SPSS in de schermen van de module Linear Regression de variabelen ‘vetpercentage’ als afhankelijke (dependent) variabele opgeven, en de variabele leeftijd als onafhankelijke (independent), dan zullen de volgende tabellen worden gegenereerd: Model Summary, ANOVA en Coeficients. NB: in de hierna volgende voorbeelden worden sommige SPSS tabellen in verkorte vorm weergegeven.
| Model Summary | ||||
|---|---|---|---|---|
| Model | R | R square | Adjusted R square | SE of the estimate |
| 1 | .821 | .659 | .645 | 6.3898 |
De tabel Model Summary geeft de Pearson’s correlatie weer tussen de betreffende en variabelen. De kolom 'R square' is een zogenaamde goodness-of-fit maat. Deze maat geeft uitdrukking aan hoe goed de geobserveerde data clusteren rond de geschatte regressielijn. In een enkelvoudige lineaire regressie is dat het kwadraat van de correlatie. De proportie wordt meestal in een percentage ‘verklaarde variantie’ uitgedrukt. In dit voorbeeld betekent R square dus dat de totale variatie in vetpercentages voor 66% verklaard kan worden door de lineaire regressie c.q. de verschillen in leeftijd.
| ANOVA | |||||
|---|---|---|---|---|---|
| Model | Sum of squares | df | Mean Square | F | Sig. |
| 1 | |||||
| Regression | 1818,362 | 1 | 1818,362 | 44,535 | ,000 |
| Residuals | 939,078 | 23 | 40,829 | ||
| Total | 2757,440 | 24 | |||
De F-test in de ANOVA tabel toets de nulhypothese: regressiecoëfficiënt b = 0 (‘er is geen samenhang tussen en , dus de regressielijn loopt horizontaal - zonder helling - door de puntenwolk’). Uit de tabel kunnen we opmaken dat leeftijd een significante voorspeller is van het gemeten vetpercentage (regressiecoëfficiënt b ≠ 0). Of, anders geformuleerd, we kunnen concluderen dat het vetpercentages van de proefpersonen significant verklaard kunnen worden door hun verschillen in leeftijd.
| Coefficients | |||||
|---|---|---|---|---|---|
| Unstandardized
coefficients |
t | Sig. | |||
| model | B | SE | |||
| 1 | (Constant) | 2,507 | 3,932 | ,638 | ,530 |
| Leeftijd | ,549 | ,082 | 6,673 | ,000 | |
a. dependent variable: vetpercentage
De t-test in de derde tabel – Coefficients- geeft niet meer informatie dan hetgeen we al wisten uit de F-test in de ANOVA tabel, namelijk dat leeftijd een significante voorspeller is van het gemeten vetpercentage. In deze tabel wordt de lineaire vergelijking weergegeven. De regressiecoëfficiënt a zien we (enigszins verwarrend in SPSS) staan onder de kolom B, rechts van de cel ‘Constant’, en heeft de waarde 2,51. Regressiecoëfficiënt b wordt ook onder de kolom B vermeld, rechts van de variabele ‘leeftijd’, en heeft de waarde 0,55. We kunnen nu de lineaire vergelijking als volgt invullen: vetpercentage = 2,51 + (0,55 leeftijd). Het verwachte vetpercentage van een proefpersoon van 60 jaar oud is dus: 2,507+ (0,549 60) = 35,45%.
Hoe werkt meervoudige lineaire regressie?
Bij meervoudige ('multiple' of 'multivariable') lineaire regressie zijn we geïnteresseerd in het gelijkertijd modelleren van twee of meer onafhankelijke variabelen. Je kunt je voorstellen dat niet alleen de leeftijd, maar ook het geslacht van de proefpersoon een bijdrage levert aan de voorspelling van zijn of haar vetpercentage. Ander voorbeeld: omdat er een associatie is tussen de lengte en het gewicht van een kind, willen we in een onderzoek naar de relatie tussen gewicht en systolische bloeddruk ook de lengte van het kind in de statische analyse betrekken. Kortom, we passen meervoudige lineaire regressie toe om:
- de waarde van een afhankelijke variabele te voorpellen met (te verklaren uit) een set van onafhankelijke variabelen, en/of
- na te gaan in welke mate een onafhankelijke variabele lineair gerelateerd is aan de afhankelijke variabele, rekening houdend met (geadjusteerd voor) de invloed van andere variabelen.
In de meervoudige lineaire regressievergelijking
zijn de verklarende variabelen of covariaten, is de afhankelijk variabele, en vormen de (partiële) regressiecoëfficiënten; is representeerd weer de residuele fout (de afstand van de datapunten tot de regressielijn). De coëfficiënt geeft aan hoeveel toeneemt als met één eenheid toeneemt, rekening houdend met (geadjusteerd voor) de invloed van de andere variabelen door die constant te houden. Op deze wijze kunnen we dus de impact van op analyseren onafhankelijk van de invloed van de andere variabelen.
Hoe interpreteer ik mijn SPSS output bij gebruik van een meervoudig lineair model?
Laten we ervan uitgaan dat we bij 100 kinderen een onderzoek doen naar de relatie tussen gewicht en systolische bloeddruk. We weten dat er een relatie is tussen het gewicht en de lengte van een kind, en mogelijk speelt het geslacht ook een rol. In een meervoudig lineaire regressie analyseren we nu het effect van gewicht (kg), lengte (cm) en geslacht (0 = jongen; 1 = meisje).
| Model Summary | |||
|---|---|---|---|
| Model | R | R square | Adjusted R square |
| 1 | .564 | .318 | .297 |
a. Adjusted R square betekent dat bij berekening van de verklaarde variantie rekening is gehouden met het aantal verklarende variabelen in het model.
Uit de Model Summary komt naar voren dat de adjusted R square = 0,297. Met andere woorden; ongeveer 30% van de variatie in systolische bloeddruk kan verklaard worden door verschillen in gewicht, lengte en geslacht van de kinderen.
| ANOVA | |||||
|---|---|---|---|---|---|
| Model | Sum of squares | df | Mean Square | F | Sig. |
| 1 | |||||
| Regression | 2804,045 | 3 | 934,682 | 14,952 | ,0001 |
| Residuals | 6001,261 | 96 | 62,513 | ||
| Total | 8805,306 | 99 | |||
De F-test in de ANOVA tabel toets de nulhypothese: regressiecoëfficiënten zijn 0. Uit de analyse komt naar voren dat er een significante lineaire relatie is tussen de systolische bloeddruk en minstens één van de onafhankelijke variabelen.
| Coefficients | |||||
|---|---|---|---|---|---|
| Unstandardized
coefficients |
t | Sig. | |||
| model | B | SE | |||
| 1 | (Constant) | 75,211 | 17,118 | 4,641 | ,0001 |
| Gewicht | 1,180 | ,261 | 4,512 | ,0001 | |
| Lengte | -,031 | ,172 | -,181 | ,857 | |
| Geslacht | 4,230 | 1,611 | 2,626 | ,010 | |
De t-test laat zien dat de relatie tussen gewicht en systolische bloeddruk significant is (p < 0,001). Geadjusteerd voor de effecten van lengte en geslacht, leidt 1 kilogram gewichtstoename tot een gemiddelde systolische bloeddrukstijging van 1,18 mmHg. Geadjusteerd voor de invloeden van gewicht en geslacht is de relatie tussen lengte en systolische bloeddruk echter niet significant (p = 0,86). Er is ook een significante relatie (p = 0,01) tussen geslacht en bloeddruk: meisjes hebben - gemiddeld genomen – een 4,23 mmHg hogere systolische bloeddrukwaarde dan jongens, rekening houdend met verschillen in gewicht en lengte tussen kinderen. Kortom, gewicht en geslacht blijken onafhankelijke voorspellers te zijn van de systolische bloeddruk. Met behulp van de gegeven regressiecoëfficiënten uit de tabel kunnen we de lineaire vergelijking verder invullen. Zo is de verwachte systolische bloeddruk van een meisje van 37 kg met een lengte van 115 cm: 75,21 + (1,18 37) – (0,03 115) + (4,23 1) = 119,65 mmHg.
Hoe interpreteer ik de resultaten van mijn lineaire model bij een log transformatie van de uitkomstmaat?
Ik heb een vraag over de interpretatie van de B-waarden in mijn lineaire regressie analyse. De afhankelijke variable is namelijk een log-getransformeerde cortisolwaarde waardoor de B waarde (en wellicht ook de gestandaardiseerde Beta) moeilijker te interpreteren zijn. Ik heb daarom de B-waarden terug getransformeerd (Transformed B (EXP(B-waarde)) en krijg dan waarden rond de 1. Mijn vraag is nu: hoe leg ik de B-waardes uit tijdens de presentatie op een congres komende week? Normaal gesproken spreek je van bij 1 unit toename in de afhankelijke variabele van ...(B-waarde) afname in cortisol waarde. Zelf dacht ik dat bijvoorbeeld nu Transformed [EXP(beta)] = 0.97, CI (0.95-0.99), p = .027 nu uiteglegd kan worden als:bij iedere unit toename van de afhankelijke variabele geeft een afname van 3% in cortisol. Klopt dit?
Als je een linear model fit om het effect van X op de log-getransformeerde cortisolwaarde te beoordelen, ziet dat er als volgt uit:
log(cortisol) = intercept + B * X
Inderdaad, een unit toename in X geeft B toename van de log(cortisol). Als we dit terug willen vertalen naar "gewone" cortisolwaardes, gebruiken we de inverse van de log:
Exp(log(coritsol)) = exp (intercept + B*SRIP)
Dit is gelijk aan:
cortisol = exp ( intercept + B*SRIP)
Bekijken we nu het verschil in cortisolwaarden bij toename van 1 unit SRIP:
cortisol = exp ( intercept + B*X + B)
Dan is dit gebruik makend van de rekenregels gelijk aan
exp (intercept + B*X) * exp (B)
Nu is het eerste gedeelte van bovenstaande vergelijking precies gelijk aan de cortisolwaarde op het "beginpunt", dus inderdaad: een unit extra SRIP geeft vermenigvuldiging van de cortisolwaarde met de factor exp(B). En ook inderdaad: indien de exp(B) = 0.97, dan geeft vermenigvuldiging hiermee een afname van 3%.
Je interpretatie was dus juist. (In het bovenstaande ben ik wel vanuit gegaan dat de cortisol waardes met de natuurlijke logaritme getransformeerd zijn en niet bijvoorbeeld met een 10log).
Zie voor uitgebreidere uitleg over het interpreteren van regressiecoefficienten bij gebruik van een log transformatie deze pagina van UCLA: Academic Technology Services, Statistical Consulting Group.
Waar vind ik lineaire regressie in SPSS?
Je vindt lineaire regressie in SPSS 16 onder Analyze -> Regression -> Linear.
Hoe geef ik categorische variabelen mee bij lineaire regressie in SPSS?
Voor het gebruiken van categorische variabelen als voorspeller in een lineair model moeten er in SPSS eerst dummy variabelen aangemaakt worden. Om bijvoorbeeld het effect van roken (met categorien 'no', 'previous' of 'current') op systolische bloeddruk te onderzoeken, moeten er twee dummy variabelen aangemaakt worden. Als we de groep die nooit gerookt heeft als referentie beschouwen, dan maken we een 0/1 variabele voor 'previous smoker' en een 0/1 variabele voor 'current smoker'. In het algemeen geldt: bij n categorien moeten n-1 dummy variabelen aangemaakt worden. In de output vinden we nu het voor het verschil previous vs no smoking en current vs no smoking de regressiecoefficient met bijhorende significantietest. Eventueel kan de "overall test" die weergeeft of de variabele roken uberhaupt bijdraagt aan het model verkregen worden door de voorspellers in twee blokken mee te geven aan het regressie model. Een blok met alle variabelen behalve roken en in een tweede blok de twee roken dummies toegevoegd. Als er bij 'Statistics' 'R squared change' staat aangevinkt, dan geeft SPSS ook een p-waarde behorend bij het toevoegen van alle drie de rook-categorien.
Alternatief kun je in plaats van de standaard Analyze -> Regression -> Linear procedure gebruik maken van de Analyze -> General Linear Model -> Univariate module. Hierin kun je aangeven wat de categorische variabelen zijn door deze als 'Fixed factor(s)' aan te duiden, de numerieke voorspellers meld je onder 'Covariate(s)'. Onder 'Model...' geef je vervolgens aan welke termen je in het model wilt, plus eventuele interacties. Vraag onder 'Options' om de parameter estimates om de gebruikelijke regressiecoeffcienten in de output te zien. Deze module doet hetzelfde als een gewone lineaire regressie, maar heeft meer opties/mogelijkheden die vaak niet van toepassing zijn.
Mijn voorspeller is niet normaal verdeeld, kan ik nu nog lineaire regressie gebruiken?
Ik heb een onderzoek gedaan bij patienten met neurologische afwijking, deze patienten kunnen afwijkingen in de hersenen hebben. Daarom heb ik een MRI van de hersenen gemaakt en een aantal neuropsychologische testen gedaan. Ik wil onderzoeken of kinderen met véél afwijkingen ook slechter scoren op de neuropsychologische testen. De variabele die de MRI afwijkingen aangeeft is niet normaal verdeeld: de helft van de patienten heeft geen afwijkingen (afwijkscore is 0), de andere helft van de patienten heeft afwijkingsscore 5 tot >10.000. Het liefst zou ik een aantal lineaire regressies doen met als voorspeller de awfijkscore en als uitkomst telkens één van de neuropsychologische testen. Een deel van de neuropsychologische testen zijn afhankelijk van de leeftijd, die moet dan dus ook mee in het model als voorspeller. Ik twijfel of ik wel een (multipele) lineaire regressie mag doen gezien de scheve verdeling van de afwijkvariabele. Logtransformeren helpt wel iets maar dan nog is het niet normaal verdeeld. Is er nog een oplossing te vinden zodat ik wel de (multipele) lineaire regressie kan uitvoeren? Een alternatief is een simpel correlatie model maken, dat kan ik non-parameterisch mbv een Spearman's correlatie doen. Volgens mij mag ik dan gewoon de ongetransformeerde afwijkscore nemen als variabele en kijken wat de Spearman's correlatie is met de neuropsychologische testen. Klopt dat? Maar dan heb ik een probleem in die gevallen waarbij ik de leeftijd ook moet meenemen als variabele, dan moet ik partial correlations doen en dan leeftijd als 'controlling for' variabele meenemen. Maar dat is weer niet non-parametrisch, is er een manier om dat te omzeilen?
Heel sec bekeken hoeft de voorspeller in een lineaire regressie niet normaal verdeeld te zijn. Die voorwaarde geldt voor de uitkomstmaat (of eigenlijk voor de residuen van uitkomstmaat minus modelvoorspelling). Echter, als je de afwijkscore als numerieke covariaat in het model zou gebruiken, dan maak je wel een andere ferme aanname, namelijk dat iedere 1 punt toename in afwijkscore met een vaste toe- of afname op de uitkomsten van de neuropsychologische testen correspondeert. En dit is gezien de grote speiding in afwijkingswaarden waarschijnlijk niet realistisch. De schattingen in zo'n regressie zouden onevenredig zwaar beïnvloed worden door de patienten met >10000 score.
Een niet-parametrische Spearman correlatie berekenen kan inderdaad. Hierbij heb je zoals je zelf al aangeeft echter geen mogelijkheid tot corrigeren voor andere factoren (de partial correlaties zijn eigenlijk gewoon multipele lineaire regressies).
Wat je alternatief zou kunnen doen is het opdelen van de afwijkvariabele in categorien. Een grove indeling in wel of geen afwijking zou kunnen, of een meer fijnmazige in bijv 0, >0 tot 50, >500. Het liefst gebruik je 'logische afkappunten'. Let er wel op dat er nog een redelijk aantal patienten in ieder van de categorien valt om het schatbaar te houden. Een regressie met deze categorische variabele als voorspeller kan dan kijken of het behoren tot een andere categorie voorspellend is voor de testuitkomsten. Hierbij is het weer mogelijk te corrigeren voor andere factoren. Ook zou je kunnen proberen om dmv een transformatie de variabele minder scheef verdeeld te krijgen, bijvoorbeeld een logtransformatie.
Referenties
Course material on interaction and effect modification from the web based distance learning course - Regression Models as a Tool in Medical Research - International School of Quantitative Research, University of Freiburg.
Terug naar OVERZICHT voor een overzicht van alle statistische onderwerpen op deze wiki.
Terug naar KEUZE TOETS voor hulp bij het uitzoeken van een geschikte toets of analyse.