Survival analyse

Auteur	ir. N van Geloven
Co-Auteur	dr. R.B. Geskus
auteurschap op deze site

Survival analyse wordt gebruikt voor data die informatie geeft over de tijd tot het optreden van een bepaald event. Met tijd wordt in deze bedoeld het aantal jaren, maanden of weken vanaf de start van de follow-up van een patient tot aan het optreden van een event. Het event kan overlijden zijn (vandaar de naam survival analyse), maar ook een relapse, herstel of een ander helder gedefinieerd eindpunt. In het algemeen wordt er bij survival analyse vanuit gegaan dat er maar één type risico is en dat een event per individu maar hoogstens één keer kan optreden. Bij meerdere risico's of meerdere herhalingen van een event zijn meer geavanceerde analyse technieken nodig zoals recurrent event analyse of competing risk analyse.

Bij het meten van tijd-tot-event data is vaak sprake van gecensureerde waarnemingen. Hierbij heb je iets aan informatie over de 'survival time' van een patient, maar weet je niet precies hoe lang de tijd-tot-event is. Een voorbeeld. Stel dat in een studie patienten over een periode van twaalf weken gevolgd worden. Censurering (Eng.: censoring) kan op drie manieren optreden:

• Een patient is gevolgd vanaf het begin van de studie tot aan het eind van de 12 weekse studie periode. Op dat moment heeft de patient het event nog niet gekregen. We weten nu alleen dat de tijd-tot-event van deze persoon langer is dan 12 weken.
• Een patient trekt zich terug uit de studie na 6 weken, dus voor het eind van de studieperiode. Van deze persoon weten we alleen dat de tijd-tot event langer is dan 6 weken. Of een patient start aan de studie maar raakt na het laatste contact op 8 weken 'lost to follow up'. Ook van deze patient weten we alleen dat de eventvrije periode langer is dan 8 weken.
• Een patient kan niet tot het einde gevolgd worden doordat hij een ander type event krijgt. Bijvoorbeeld: we onderzoeken tijd tot relapse na operatie, maar een patient overlijdt tijdens de studie zonder een relapse gehad te hebben.

Kaplan Meier analyse

Wanneer gebruik ik een Kaplan Meier analyse?

Om de tijd tot het optreden van het event voor de gehele steekproef te kwantificeren, wordt er vaak een Kaplan Meier analyse gebruikt. De Kaplan Meier analyse is een niet-parametrische aanpak. Dat wil zeggen dat er geen aanname gedaan wordt ten aanzien van het soort verdeling (normaal, gamma etc.) van de event tijden. Toch zitten er wel een paar aannames achter deze methode:

• De prognose van patienten die vroeg of laat zijn geïncludeerd in de studie is gelijk.
• Patienten die gecensureerd zijn op een bepaald tijdstip hebben dezelfde prognose als patienten die op datzelfde tijdstip wel in de studie zijn gebleven (en op dat moment nog geen event hebben gehad). Er wordt niet aan deze aanname voldaan als bijvoorbeeld personen met een grote kans op een event vlak voordat het event optreedt de studie verlaten.
• De tijdstippen waarop de events optreden zijn exact bekend.
• Patienten worden vanaf het begin van de onderzochte periode gevolgd. Als er bijvoorbeeld pas 10 dagen na interventie gestart wordt met het volgen van survival stutus van patienten, dan zullen patienten die in de eerste 10 dagen reeds overleden zijn niet vertegenwoordigd zijn in de studie. Een Kaplan-Meier analyse geeft dan geen goede inschatting van de echte survival tijd. Survival modellen die rekening houden met dit verschijnsel worden late entry survival modellen genoemd.

De basis gedachte achter de Kaplan Meier procedure is het opdelen van de tijdsschaal. Op ieder moment dat er bij één of meerdere patienten een event optreedt, wordt de kans daarop geschat door het aantal events op dat moment te delen door het aantal personen dat op dat moment nog in de studie zit (i.e. niet eerder al een event heeft gehad of gecensureerd is). De survival functie (of cumulatieve proportie van 'survivors') combineert deze schattingen over alle tijdstippen. Op deze manier wordt het resultaat minimaal beïnvloed door patienten die halverwege de rit gecensureerd raken. Een Kaplan-Meier analyse resulteert in een 'life table' en een survival curve.

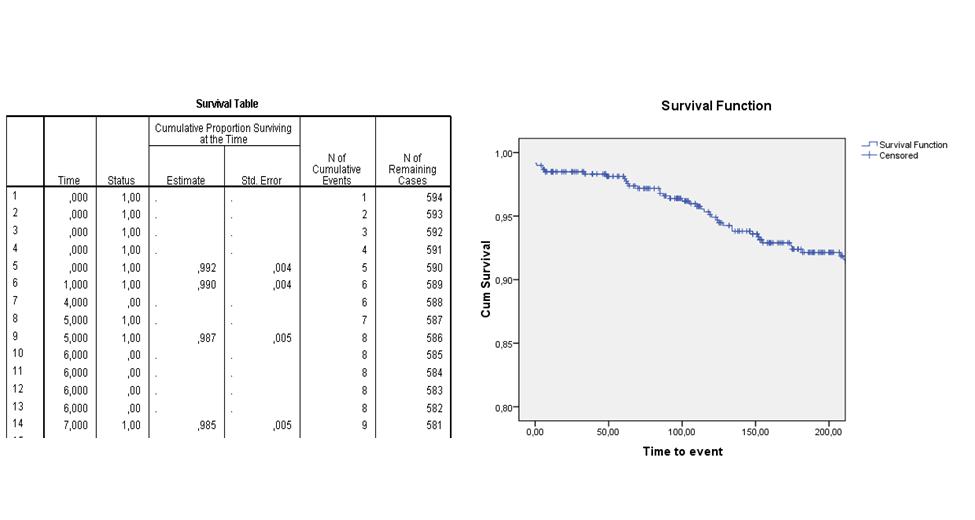
De volgende life table en survival curve laten bijvoorbeeld zien wat de verwachte overlevingskans is van patienten die een dotterbehandeling hebben ondergaan. Je ziet in de tweede kolom ("Time") van de life table dat er op dag 4 en dag 6 patienten gecensureerd raakten en dat er op dag 0 vijf events waren, op dag 1 een event, op dag 5 twee events en dag 7 een event optrad. Op de dagen dat er een event optrad, is de cumulatieve survival berekend. In de survival curve zie je de geschatte survival functie over de eerste 200 dagen na interventie. Na 200 dagen wordt de kans op overleven geschat op ongeveer 92%.

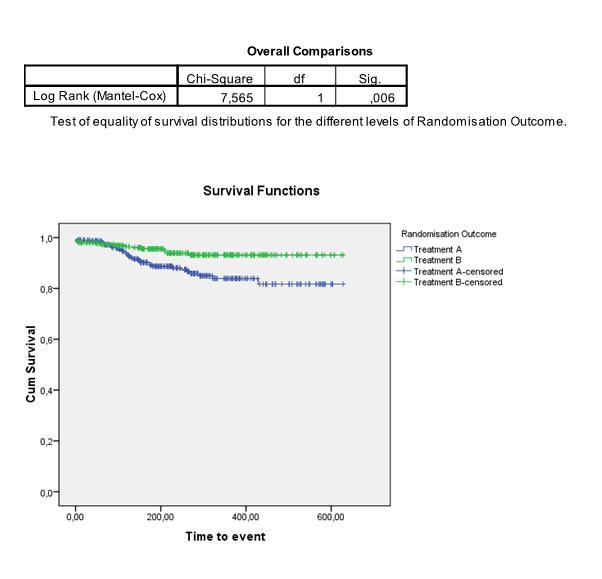
Hoe test ik of Kaplan Meier survival curves van elkaar verschillen?

We kunnen de curves ook apart schatten en vergelijken voor twee (of meer) subgroepen in onze data. Om te testen of de Kaplan Meier curves van 2 (of meer) groepen significant van elkaar verschillen, wordt vaak de log-rank test gebruikt. Hierbij is de nulhypothese dat de curves niet van elkaar verschillen. De test vergelijkt de geobserveerde verschillen tussen de survival curves met verschillen die zouden kunnen ontstaan als er geen verschil is tussen de groepen. In het volgende voorbeeld concluderen we bijvoorbeeld dat het verschil tussen treatment A en treatment B significant is:

Kan ik meerdere aparte Kaplan Meier curves bij elkaar in 1 grafiek plotten?

Voor een paper heb ik 3 kaplan meier curves die op de x-as allemaal even ver lopen (allemaal een tijdsduur van 27 maanden). Ik wil deze 3 curves in 1 plot zetten. Kan dat met SPSS en zo ja, hoe?

We zijn er zelf uitgekomen en wel op de volgende manier: In ons geval wilden wij 3 verschillende curves (survival, grote amputatie en kleine amputatie) in 1 KM grafiek zetten. We hebben de data opnieuw gerangschikt. 1 variable met time to event, 1 variable met event status (alledrie de events hadden status 1), en een nieuwe onderscheidende variable die duidelijk maakte dat de eerste time to event en event zelf sloeg op survival, tweede time to event en event zelf op grote ampuatie en drede time to event en event zelf op kleine amputatie. Invoeren gewoon time to event en event status en de nieuwe onderscheidende variable wordt de 'factor'. Mocht iemand anders ooit nog met hetzelfde probleem zitten, bij deze de oplossing.

Hoe kan ik mijn logrank analyse doen over alleen het eerste jaar van de follow up?

Op een polikliniek voor HIV-geinfecteerde kinderen in Malawi hebben we in de periode van 2004-2008 een cohort kinderen gevolgd vanaf het moment dat zij startten met antiretrivirale therapie. We zijn geinteresseerd in hun uitkomsten en risicofactoren voor mortaliteit en uitval uit behandeling (LTFU). 1) Ik probeer uitkomsten na 12 maanden op een rij te zetten dmv analyze_survival_lifetables. Dit lijk te lukken. 2) Ik wil naar voorspellende factoren kijken voor overlijden en dood op 12 maanden. Voor univariate analyses zou ik hiervoor willen gebuiken: analyze_survival -> kaplanmeier met compare factor log-rank test. Hiermee doe ik een analyse voor uitkomst na totale duur folllow up. Het lukt mij niet hierbij specifiek naar uitkomsten tot 12 maanden te kijken.

Als er een langere follow up is, en je wilt in een analyse alleen focussen op de periode tot 12 maanden, dan is het nodig om de informatie van de personen op 12 maanden te censureren. Als het goed is heb je nu in de dataset de volgende 2 variabelen:

-tijd tot laatste follow up of tijd tot optreden event (mortaliteit of uitval behandeling): FUtime

-event indicator (wel of niet het event opgetreden): FUstatus (1=event, 0= geen event)

Om alleen op de eerste 12 maanden te focussen, is het nodig om de volgende aanpassingen te maken:

indien FUtime>12 en FUstatus =0 -> FUtime=12 FUstatus=0

indien FUtime>12 en FUstatus =1 -> FUtime=12 FUstatus=0

indien FUtime=<12 en FUstatus =1 -> variabelen blijven hetzelfde

indien FUtime=<12 en FUstatus =0 -> variabelen blijven hetzelfde

Met de nieuwe FUtime (die nooit groter is dan 12) en de nieuwe status (die nu iets minder events bevat) kan een Kaplan-Meier analyse gedaan worden voor alleen het eerste jaar.

Hoe ga ik om met patienten die vanwege overlijden niet meer het event van interesse kunnen krijgen?

Ik heb een RCT gedaan met een follow-up van 1 jaar met als belangrijkste uitkomstmaat: het aantal dagen vanaf randomisatie tot terugkeer naar werk. Nu wil ik onderzoeken of de tijd tot terugkeer naar werk significant verschilt tussen beide groepen (controlegroep en interventiegroep). Hiervoor heb ik KM-survival analyse gedaan met Log rank toets. Nu is het zo dat een aantal patiënten gedurende de follow-up periode overleden zijn en een aantal patiënten palliatief worden behandeld. Deze patiënten kunnen de positieve uitkomstmaat (weer aan het werk) nooit meer bereiken. Hoe ga je om met deze patiënten in de survival analyse? Moet ik deze patiënten helemaal uit de analyse halen? Moet ik deze als censored beschouwen? Moet ik deze patiënten zien als negatieve uitkomst (=niet aan het werk). Kortom wat is het effect van censored data op een survival analyse en logrank toets en welke afweging is het meest juist?

De voor- en nadelen van de verschillende alternatieven:

1. de overleden/palliatieve patienten in de KM-analyse laten en censureren op het moment van dit event

Voordeel: de informatie van deze patienten voordat ze overleden / voordat ze palliatief waren doet mee in de analyse / geen verlies van data Nadeel: de KM-analyse veronderstelt dat de prognose van deze patienten, nadat ze gecensureerd worden, gelijk is aan patienten die nog wel in de analyse zitten (aanname van non-informative censoring). De schattingen (en vergelijkingen) op latere follow up momenten worden daardoor (onevenredig) veel bepaald door relatief goede patienten die wellicht niet representatief zijn voor de totale groep.

2. de overleden/palliatieve patienten in de KM-analyse uit de analyse laten

Voordeel: eenvoudig uit te leggen aanpak, je beperkt de studiegroep alsware het een exclusiecriterium is Nadeel: alleen als op t=0 al bekend is dat iemand tot de 'exclusiegroep' behoort is dit een logische aanpak, voor deze personen zou je kunnen zeggen dat de interventie toch geen invloed meer kan hebben op terugkeer naar werk omdat dat (ongeacht welke behandeling ook) geen resultaat hierop kan hebben. Voor personen die in het begin nog alle kanten op kunnen en pas later achteruit gaan zou het zonde zijn/kan het vertekening geven die info niet te gebruiken.

3. de overleden/palliatieve patienten in de KM-analyse als negatieve uitkomst zien / Competing risk analyse

Voordeel: Je zou kunnen ageren dat deze patienten een ultiem 'slechte' uitkomst hebben en ook als zodanig meegerekend moeten worden. Je zegt dan eigenlijk dat ze het event 'terug naar werk' nooit meer zullen bereiken. Hun status staat dan op 0, en de follow up tijd zou je (gekunsteld) op oneindig lang kunnen zetten (of iig langer dan de langste follow up). Je kunt dit ook formeel in een competing risk analyse doen. Nadeel: de analyse is minder standaard / competing risk analyse wordt niet standaard in SPSS aangeboden.

Hoe bereken ik de 'events per person year'?

'Ik wil graag mijn uitkomsten (opnames in verband met verklevingen in de buik en het vóórkomen van littekenbreuken) weergeven als 'event per person-years at risk', om te corrigeren voor de wisselende follow up duur. Hoe kan ik dit het beste doen? Ik zou een Kaplan-Meier kunnen maken van time-to-event, maar ik wil ook graag deze maat weergeven. Moet ik dan een variable aanmaken waarin ik event ja/ nee deel door de tijd 'at risk'? Of is er een functie in SPSS waarmee ik dit makkelijker kan berekenen?

De uitkomst 'events per person-years at risk' is simpel te berekenen door alle events bij elkaar op te tellen (som_events), alle tijd at risk bij elkaar op te tellen (som_tijd) en die twee op elkaar te delen: som_events/som_tijd.

Omdat SPSS gewend is om te rekenen 'per rij' en niet zozeer per kolom, zijn deze optellingen makkelijker te doen als je de data even in een ander pakket (excel of R) zet.

Bij de maat 'events per person-years at risk' wil je waarschijnlijk ook een betrouwbaarheidsinterval berekenen? Die zou je kunnen berekenen mbv de calculator op www.openepi.com. Kies in de linkerbalk voor person time -> 1 rate. Geef het aantal events en de totale tijd in. Je krijgt dan de rate en een betrouwbaarheidsinterval terug. Let goed op, de rate wordt per 10, 100, 1000 person years gegeven (afhankelijk van het aantal informatieve decimalen). Het is dus goed om de getallen naast je eigen berekening (zoals boven) te leggen.

Waar vind ik de Kaplan Meier analyse in SPSS?

Je vindt de Kaplan Meier analyse in SPSS 16 onder Analyze -> Survival -> Kaplan-Meier.

Cox regressie

Wanneer gebruik ik een Cox proportional hazards model?

Wanneer er bij een survival analyse slechts één voorspellende factor onderzocht wordt die slechts een paar mogelijke waardes kan aannemen, kan een Kaplan Meier analyse volstaan. Zijn er echter meerdere factoren die de overleving kunnen beinvloeden, dan is een uitgebreider model nodig. Een veel gebruikt model is het Cox proportional hazards model. Hiermee kun je net als met andere multivariabele regressie modellen meerdere voorspellers tegelijk bestuderen. Voordeel van het Cox model boven een Kaplan Meier analyse is bovendien dat er naast de vraag "is er een effect" ook antwoord gegeven wordt op de vraag "hoe groot is het effect" van een bepaalde voorspeller. Het Cox model geeft de grootte van een effect weer met behulp van hazard ratio's (HR), waarbij een HR van 1 aangeeft dat er geen verschil is. De hazard is de instantane kans om een event te krijgen, en een hazard ratio is vergelijkbaar met een relatief risico. Bijvoorbeeld: "During the 20-year follow-up, 83 women developed lung cancer. There was a moderate association between hormone use and lung cancer (hazard ratio, 1.13; 95% CI, 1.08-1.73)."

Het Cox model maakt een belangrijke aanname: de proportional hazards assumptie. Deze zegt dat de HR's constant zijn in de tijd. Dit betekent dat het relatieve verschil in hazard veroorzaakt door verschillende waardes van een voorspeller gelijk blijft in de tijd. Er wordt in het bovenstaande voorbeeld dus vanuit gegaan dat het wel of niet gebruiken van hormonen een zelfde invloed heeft na 1 jaar als na 20 jaar follow up: op ieder tijdstip wordt de kans op het optreden van longkanker bij hormoongebruik 1.13 keer hoger geschat dan dezelfde kans als er geen hormonen werden gebruikt.

Hoe test ik de proportional hazards aanname binnen een Cox model?

Er zijn meerdere manieren om de PH aanname van een Cox model te testen:

• Grafisch

Als een variabele in het model voldoet aan de proportional hazards (PH) aanname, dan zullen de geschatte overlevingscurves, op de zogenaamde log-schaal, voor de waardes van deze variabele parallel lopen. Je kunt hier naar kijken door in het cox model de variabele voor welke je de PH aanname wilt onderzoeken niet meer als covariaat, maar als stratum mee te geven en te vragen om log minus log survival plots. De resulterende lijnen moeten op het oog parallel lopen (zeker elkaar niet kruisen) om te voldoen aan de PH aanname voor deze variabele. Voor iedere variabele in het model is een dergelijke plot nodig. In deze voorbeeldsyntax kun je zien hoe het maken van een log minus log plot er in SPSS syntax uit komt te zien.

• Testen van (Schoenfeld) residuen

Er kan een formele test gedaan worden mbv Schoenfeld residuen. Er is geen standaard functie hiervoor in SPSS. In Stata (functie estat phtest) of R (functie cox.zph) kan het wel direct. Download hier een script voor het testen van de PH aanname in R.

• Toevoegen van een tijdsafhankelijke variabele

Anticiperend op het mogelijk niet voldoen aan de PH aanname kun je ook een time dependent Cox model draaien met daarin een tijdsafhankelijke variabele opgenomen (bijvoorbeeld GENDER*T). Als deze tijdsafhankelijke variabele significant bijdraagt aan het model, is er blijkbaar niet aan de PH aanname voldaan.

Hoe kan ik de output lezen van de analyse van een categorische variabele?

Voor een cohort HIV geinfecteerde kinderen, gevolgd vanaf het moment dat ze met antiretrovirale medicatie starten, ben ik op zoek naar voorspellers van overlijden. Ik ben nu bezig met de Cox regressie (vooralsnog bezig met univariate analyse). Hieronder een voorbeeld van output van een categoriale variable (leeftijdscatgorieën) met meer dan 2 categorieën (referentie = kinderen>12 van wie we verwachten dat ze de beste prognose hebben) (1) (2) (3) betreffen 0-1jaar, 1-5jaar en 5-12jaar oude kinderen.

Variables in the Equation
		B	S.E.	Wald	df	Sig.	Exp(B)	95.0% C.I.for Exp(B)
								Lower	Upper
Leeftijd	leeftijd			23.539	3	.000
	leeftijd(1)	1.094	.261	17.613	1	.000	2.985	1.791	4.795
	leeftijd(2)	.773	.211	13.379	1	.000	2.166	1.431	3.276
	leeftijd(3)	.351	.236	2.206	1	.137	1.420	.894	2.256

De eerste regel laat het resultaat zien van de overall test voor de variabele. Dit is de test die als nulhypothese heeft dat alle 4 de categorieën dezelfde kans (eigenlijk hazard) hebben op overlijden. De toets kijkt of er ergens een verschil is in categorieën, je ziet ook dat de test 3 'degrees of freedom' heeft. Je kunt het vergelijken met een ANOVA test bij het vergelijken van gemiddelde waarden in 4 groepen. De test hoort dus niet specifiek bij de referentiecategorie, dat vindt SPSS gewoon een handige locatie om 'm neer te zetten. In principe ga je als volgt te werk: je kijkt eerst of de overall test significant is. Als dat zo is, dan ben je geoorloofd om door te gaan en te kijken naar de verschillen tussen de categorieën onderling.

Waar vind ik het Cox proportional hazards model in SPSS?

Je vindt de Kaplan Meier analyse in SPSS 16 onder Analyze -> Survival -> Cox Regression of Cox w./ Time Dep Cov.

Referenties

• Altman DG, Bland JM. Time to event (survival) data. BMJ 1998;317:468-9.
• Bland JM, Altman DG. Survival probabilities. The Kaplan-Meier method. BMJ 1998;317:1572.
• Bland JM and Altman DG. The log rank test. BMJ 2004;Vol 328 may 2004.
• An Introduction to Survival Analysis - by Mark Stevenson from EpiCentre, IVABS, Massey University. 44 pagina's cursusmateriaal (Engels) met voorbeeld syntax in R plus 100 pagina's aan voorbeeld artikelen.
• Hosmer, D. W., and S. Lemeshow. 1999. Applied Survival Analysis. New York: John Wiley and Sons.
• Kleinbaum, D. G. 1996. Survival Analysis: A Self-Learning Text. New York: Springer-Verlag.
• Norusis, M. 2004. SPSS 13.0 Advanced Statistical Procedures Companion. Upper Saddle-River, N.J.: Prentice Hall, Inc..

Terug naar OVERZICHT voor een overzicht van alle statistische onderwerpen op deze wiki.

Terug naar KEUZE TOETS voor hulp bij het uitzoeken van een geschikte toets of analyse.