Herhaalde metingen

Auteur	ir. N van Geloven
Co-Auteur	prof. dr. A.H. Zwinderman
auteurschap op deze site

Wat zijn herhaalde metingen?

Herhaalde metingen zijn meerdere metingen van dezelfde variabele bij dezelfde persoon/patient, proefdier, of algemeen geformuleerd, dezelfde observationele eenheid. Voorbeelden:

• herhaling in de tijd: als patienten herhaaldelijk in een follow-up periode worden gemeten (of: voor en na een behandeling);
• meerdere locaties: metingen op meerdere locaties in het lichaam van dezelfde persoon (linker en rechter oog, meerdere coupes in een biopt, meerdere slices in een MRI beeld);
• meerdere condities: als dezelfde patient onder twee of meer verschillende condities (bijv. behandelingen) wordt gemeten, bijvoorbeeld bij een cross-over studie;
• herhalingen tbv nauwkeurigheid: als een meting een grote variatie binnen een persoon heeft (of een grote meetfout) dan kan het zinvol zijn om een aantal aparte metingen te doen;
• multilevel structuren: als metingen bij meerdere personen gedaan zijn die onderdeel uitmaken van dezelfde groep. Bijvoorbeeld patienten die dezelfde huisarts hebben, waarbij de interventie per huisartspraktijk is uitgevoerd. Het klassieke voorbeeld hier zijn leerlingen die dezelfde docent hebben en docenten die weer bij eenzelfde school horen.

Waarom kun je bij herhaalde metingen geen standaard regressie model gebruiken?

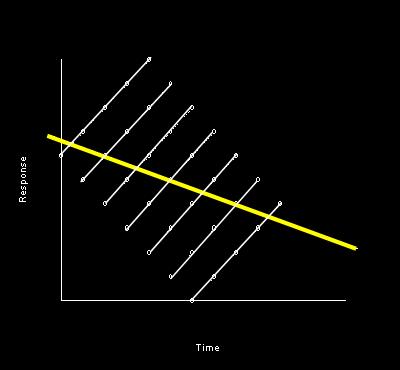
Bij een standaard regressie model wordt aangenomen dat alle metingen onafhankelijk van elkaar zijn. Bij herhaalde metingen is het waarschijnlijk dat twee metingen van dezelfde persoon meer op elkaar lijken dan twee metingen van verschillende personen. Als dat zo is, dan zijn de metingen binnen dezelfde persoon niet onafhankelijk. Als bij herhaalde metingen geen rekening wordt gehouden met deze afhankelijkheid, dan zijn i.h.a. de standaard fouten en de p-waardes (onterecht!) te klein. Bovendien kan de uitkomst van de regressie analyse volkomen fout zijn, zoals geillustreerd in het plaatje dat hieronder staat. In deze figuur worden de observaties van 6 personen getoond en elke persoon laat een duidelijk stijgende trend zien. Als de afhankelijkheid van de waarnemingen genegeerd wordt, dan is de best passende regressie lijn door de totale punten-wolk de gele dalende lijn en deze geeft geen correcte weergave van de trend per patient.

Welke analyses zijn er mogelijk voor herhaalde metingen?

• Simpele methodes: Soms kunnen herhaalde metingen samengevat worden in een enkele relevante maat. Je kunt bijvoorbeeld de meting van slechts een tijdpunt gebruiken, de verandering tussen twee meetpunten gebruiken, een samenvattende maat zoals het gemiddelde of de area under the curve uitrekenen, of de tijd tot het bereiken van een bepaald level analyseren in een survival analyse.
• Geavanceerde methodes: Methodes die wel herhaalde metingen aankunnen zijn o.a. mixed models, repeated measurements ANOVA en Generalized Estimation Equations (GEE).

De simpele methodes gebruiken maar een deel van de verzamelde informatie en dat levert vaak minder onderscheidingsvermogen (power) op. Repeated measurements ANOVA is een specifieke variant van mixed-models, maar is alleen beschikbaar voor continue normaal verdeelde afhankelijke variabelen, die op vaste en dezelfde tijdstippen zijn gemeten in alle patienten. Mixed-models en GEE-modellen zijn wat lastiger te specificeren, maar zijn flexibeler en zijn beschikbaar voor zowel continue normaal verdeelde afhankelijke variabelen, als voor bijv dichotome afhankelijke variabelen. Bovendien kunnen de mixed modellen ook omgaan met een zekere mate van missing values, namelijk wanneer de data missing at random zijn.

area under the curve

Wat is een area under the curve en wanneer kun je die gebruiken?

Wanneer er op meerdere tijdstippen metingen zijn van een patient, kun je die samenvatten in een "area under the curve". Hierbij bereken je per patient de oppervlakte onder de gemeten punten in de tijd. Deze samenvattende maat gebruik je vervolgens voor de analyse.

Hoe bereken ik met SPSS een area under the curve bij herhaalde metingen?

Ik wil graag van een bepaalde meting in de tijd, op verschillende tijdstippen gemeten, de 'area under the curve' bepalen. Ik kom er met SPSS niet uit. Ik moet er nl een stuk of 300 bepalen... heeft u nog een advies?

Je kunt de volgende syntax gebruiken, deze rekent per patient een area under the curve uit. Bovenaan het document staat beschreven hoe je de variabelen in SPSS moet hebben staan.

mixed models

Mixed models kunnen op meerdere manieren gespecificeerd worden. Het is zinvol om een onderscheid te maken tussen

1. onderzoeken waarbij alle patienten op (min of meer) dezelfde tijdstippen (of onder dezelfde condities) herhaald worden gemeten, en
2. onderzoeken waarin het aantal herhaalde metingen per patient en/of de tijdstippen en condities verschillen tussen patienten.

Situatie 1: herhaalde metingen op dezelfde momenten

Als alle patienten op dezelfde tijdstippen (onder dezelfde condities) zijn gemeten, kan het mixed-model gezien worden als een uitbreiding van een standaard lineair model. In formulevorm ziet de uitbreiding van het standaard model er als volgt uit:

Failed to parse (syntax error): {\displaystyle \begin{equation*} Y_{i,t} & = & a + b \times X_{i,t} + \epsilon_{i,t} \\ \end{equation*}}

waarbij $Y_{i,t}$ de meting van de $i^{de}$ patient is op het $t^{de}$ tijdstip (conditie); $X_{i,t}$ is de meting van de covariaat op dat moment en $\epsilon _{i,t}$ is de afstand (of: residu) van de datapunten tot de regressielijn. Bij een standaard lineaire regressie zijn al deze residuen onafhankelijk van elkaar, maar bij herhaalde metingen is dat niet per se het geval. Namelijk, als het eerste datapunt van een patient (ver) boven (of onder) de lijn ligt, is het goed voorstelbaar dat volgende datapunten van dezelfde persoon ook boven (of onder) de regressielijn zullen liggen. Anders geformuleerd: datapunten van dezelfde persoon lijken meer op elkaar dan op datapunten van andere personen. Bij een mixed model wordt rekening gehouden met de correlaties tussen de residuen van metingen bij dezelfde patient. Dit kan op verschillende manieren en moet door de gebruiker worden gespecificeerd. Veel voorkomende correlatiestructuren zijn:

• compound symmetry, waarbij aangenomen wordt dat de correlaties tussen alle residuen van dezelfde persoon gelijk zijn. De eerste en de tweede meting van een persoon hangen dus even sterk met elkaar samen als de eerste en de laatste meting van die persoon;
• unstructured, waarbij geen enkele aanname wordt gemaakt over de correlaties. Iedere correlatie tussen twee tijdspunten wordt los van de anderen bepaald;

Er zijn nog diverse andere opties en de beste keuze hangt af van het type onderzoek en het aantal herhaalde metingen. Er zijn statistische maten die je helpen bij het maken van de keuze. Vaak wordt hiervoor de Akaike Information Criterium (AIC) gebruikt. Dit is een maat voor hoe goed het gekozen model past bij de data. Hoe lager de AIC, hoe beter het model past.

Deze eerste soort uitbreiding van het standaard lineaire model wordt ook wel 'Generalized Least Squares Model' genoemd.

Situatie 2: herhaalde metingen op verschillende momenten

Als het aantal herhaalde metingen per patient en/of de tijdstippen (condities) waarop er gemeten wordt verschillen tussen patienten, ligt het voor de hand om het lineaire model op een andere wijze uit te breiden. In situatie 1 werd de correlatie tussen meetpunten op verschillende tijdstippen direct gemodelleerd. Als er niet op vaste tijdstippen gemeten wordt, is dit niet logisch. De afhankelijkheid van metingen bij eenzelfde patient kan ook gemodelleerd worden met zogenaamde random effects. Met random effects wordt een inschatting gemaakt van de afwijking die metingen van eenzelfde patient hebben ten opzichte van de regressielijn. Hierbij maakt het niet uit hoe vaak en op welke tijdstippen een patient gemeten is; al zijn metingen worden verondersteld een vaste afwijking van de 'gemiddelde' regressielijn te hebben. In formulevorm ziet dit er als volgt uit:

Failed to parse (syntax error): {\displaystyle \begin{equation*} Y_{i,t} & = & (a+ \alpha_i) + (b+\beta_i) \times X_{i,t} + \epsilon_{i,t} \\ \end{equation*}}

waarbij de nu toegevoegde $\alpha _{i}$ en $\beta _{i}$ de specifieke afwijkingen van patient $i$ t.o.v. de regressielijn voorstellen. De $\alpha _{i}$ is de afwijking van de intercept van patient $i$ ten opzichte van de gemiddelde intercept $a$. De $\beta _{i}$ is de afwijking van de helling (slope) van patient $i$ ten opzichte van de gemiddelde helling $b$ van de regressielijn. De $\alpha 's$ en $\beta 's$ worden niet direct geschat, in plaats daarvan wordt verondersteld dat zij normaal verdeeld zijn met gemiddelde 0. De standaard deviaties van deze verdelingen worden geschat. De specificaties van de random effects kunnen nog uitgebreid worden en de fit van het model wordt gekwantificeerd met bijvoorbeeld de AIC. Ook hier geldt: het model met de laagste AIC past het beste bij de data.

Deze tweede soort modellen wordt vaak aangeduid als 'Random Effect Models'.

Waar vind ik linear mixed models in SPSS?

Je vindt de linear mixed models in SPSS 16 onder Analyze->Mixed models->Linear. T/m SPSS 18 is er alleen nog een mixed model beschikbaar voor continue (normaal verdeelde) uitkomsten. Vanaf SPSS 19 biedt SPSS ook procedures aan voor andere typen uitkomsten zoals dichotome variabelen. Deze vind je onder Analyze -> Mixed Models -> Generalized. In andere pakketten zoals R (package 'nlme' en package 'lme4'), Stata (GLAMM) en SAS zijn er ook mixed modellen beschikbaar voor verschillende typen uitkomstmaten.

Let op: om een mixed model in SPSS te kunnen draaien moeten de data onder elkaar gestructureerd staan, waarbij iedere meting op een rij staat en er meerdere rijen zijn die bij dezelfde patient horen. In deze SPSS handleiding staat stap voor stap beschreven hoe data te restructureren is in het gewenste format voor mixed models. Als er drie herhaalde metingen van drie patienten zijn, ziet het resultaat er bijvoorbeeld zo uit:

patientnummer	metingnr	meting
1	1	10
1	2	9
1	3	11
2	1	8
2	2	11
2	3	12
3	1	5
3	2	8
3	3	9

De hierboven beschreven 'situatie 1' modellering gebeurt in SPSS middels het specificeren van de 'Repeated' (+bijbehorende repeated covariance type) in het eerste panel van de mixed procedure. De in 'situatie 2' besproken modellering wordt gespecificeerd onder de 'Random...' knop (let op: random intercept staat by default uit, bij covariance type kan correlatie tussen de random effects gespecificeerd worden). Vaak is het gebruik van 1 van beide opties (danwel repeated danwel random) voldoende om de correlatie in de data op te vangen. Gebruik maken van beide opties kan wel, maar zal soms leiden tot overbodige parameters.

Voorbeeld: hoe analyseer ik met een mixed model een effect in de tijd?

Ik onderzoek een groep patienten die een operatie hebben ondergaan. We zijn geinteresseerd in de pijnscore (VAS) op verschillende tijdsmomenten na de operatie. De verwachting is (uiteraard) dat de pijn direct na de operatie heviger is dan bijv. 3 mnd daarna (dit klopt ook als je de data in een barplot zet). In eerste instantie heb ik de ANOVA for repeated measures gebruikt om te analyseren of de pijn significant verandert in de tijd. Maar, omdat ik een aantal missing data heb, heb ik ook geprobeerd een mixed models analyse (hier mijn syntax) te doen. Mijn vragen hierover:

1. Heb ik de juiste covariance structure gebruikt? (nl. AR1)

2. Ik heb 'tijd' als fixed effect genomen omdat de afname van de VAS op specifieke tijdsmomenten gebeurde, klopt dat?

3. Hoe geef de resultaten van deze mixed analyse weer?

1. Of AR(1) de beste is is niet zo te zeggen, dat hangt af van de correlatie tussen de tijdsmomenten in jouw data. Je kunt bijvoorbeeld alle mogelijke structuren draaien en dan degene met de kleinste AIC te kiezen (smaller is better zoals er ook onder staat).

2. Tijd is hier inderdaad een fixed variable, want je wilt hier de hypothese toetsen of er een verandering in de tijd is.

3. In de output vind je onder "fixed effects" een B die aangeeft wat het effect is per tijdspunt (tov het startpunt) en een bijbehorende p-waarde. Dit is de toets die je waarschijnlijk wilt rapporteren. Onder het kopje "mean estimates" vind je de schatting van het model voor de gemiddelde VAS waarde op ieder tijdpunt. Deze mean estimates zijn voor een lezer makkelijker te interpreteren dan de B's.

Wat is het verschil tussen een mixed model en een GEE model?

Ik heb een mixed model gebruikt omdat ik wil corrigeren voor de familieverbanden tussen mijn patienten. In een paper met een soortgelijke analyse zie ik echter dat er een GEE model is gebruikt. Welke moet ik hebben en wat is het verschil?

Beide modellen, een mixed model en een GEE model, kunnen corrigeren voor familieverbanden (of andere herhaalde metingen structuren). Een GEE (generalized estimation equations), ook wel genoemd marginaal model, negeert de correlaties tussen de herhaalde metingen in dezelfde familie, maar corrigeert de standaardfouten van de regressie coëfficiënten door robuuste standaardfouten te berekenen. Een mixed model, ook wel conditioneel model, of ook wel random-effects model modelleert de correlaties tussen de herhaalde metingen in dezelfde familie door een random-effect per familie in het model te includeren. De herhaalde metingen in een familie hebben die random-effects parameter gezamenlijk en dat maakt dat die metingen correleren. De volgende pagina van The analysis factor geeft een helder overzicht van de overeenkomst/verschillen tussen verschillende modellen die je kunt gebruiken voor herhaalde metingen.

repeated measurements ANOVA

Repeated measurements ANOVA is een wat oudere term voor speciale vormen van mixed-models voor het analyseren van herhaalde metingen van een kwantitatieve afhankelijke variabele die normaal verdeeld is. Binnen het SPSS pakket wordt deze techniek aangeduid als GLM - repeated. Zoals eerder opgemerkt is deze procedure specifieke variant van mixed-models, maar is alleen beschikbaar voor continue normaal verdeelde afhankelijke variabelen, die op vaste en dezelfde tijdstippen zijn gemeten in alle patiënten.

Repeated measures ANOVA zoals in SPSS geimplementeerd, geeft twee soorten analyses, namelijk onder de aanname dat de correlaties tussen de herhaalde metingen allemaal dezelfde waarde hebben (compound symmetry) of zonder aannames over de correlaties (unstructured). In de SPSS output worden de compound-symmetry resultaten onder het kopje Tests of Within-Subjects Effects gerapporteerd en de unstructured resultaten onder het kopje Multivariate Tests. Wel handig is dat Mauchly's Test of Sphericity wordt gegeven; dat is een statistische toets van de nulhypothese dat de compound symmetry aanname klopt (kleine p-waardes van deze test zijn een indicatie dat compound symmetry niet goed past bij de data). Als sphericity (i.e. compound symmetry) wordt verworpen, dan kunnen ofwel de multivariate toets resultaten gebruikt worden, ofwel een Greenhouse-Geisser of een Huynh-Feldt correctie worden toegepast op de Tests of Within-Subjects Effects.

Wanneer kan ik een repeated measurements ANOVA gebruiken?

Je kunt een repeated measurements ANOVA gebruiken als:

• de afhankelijke variabele continue is en (per level van de onafhankelijke voorspeller) normaal verdeeld is,
• de herhaalde metingen op vaste tijdstippen in alle patienten zijn gedaan,
• er geen missende waardes zijn.

Hoe kan ik post hoc testen doen bij een two-way repeated measures anova?

Ik heb twee onafhankelijke groepen (patient/controle is between subject factor) waarbij bij beide op 5 tijdsmomenten data is verzameld (5 timepoints als within subject factor). Nu run ik een two-way repeated measures anova om het interactie effect tussen groep en tijd te bekijken. Indien dit significant is wil ik graag weten op welke tijdsmomenten de controle groep verschilde van de patient groep. Er is geen optie in SPSS om een Tukey post hoc test te doen. Mag je in deze situatie een independent t-test gebruiken op ieder tijdstip om te bepalen op welke verschillende tijdsmomenten de twee groepen met elkaar verschilden?

Zo niet, dan wil ik graag een Tukey met de hand uitrekenen, dit heb ik al wel gedaan voor de one-way repeated measures anova waarin ik bij de patient groep heb gekeken op welke tijdsmomenten de data verschilde met de data van de baseline meting. Maar kan je dit ook doen bij een two way anova met 2 onafhankelijke groepen?

Je kunt de losse (t-)testen doen (t0 patient minus t0 controle, t1 patient minus t1 controle etc.). En vervolgens moet je de uitkomsten van die testen corrigeren voor het feit dat je multiple comparisons doet. Ik zou daar zelf niet direct zien hoe Tukey toe te passen, omdat je daarbij uitgaat van een aantal means met hypothese dat ze allemaal (aan elkaar) gelijk zijn. Nu is het een ander geval, namelijk je wilt kijken of de means telkens 2 aan 2 gelijk aan elkaar zijn. Ik zou daarom een andere correctiemethode gebruiken (zoals Bonferroni of Bonferroni-Holms).

Let bij je eerdere analyse (post hoc op de within factor) ook goed op dat je de vergelijkingen wel gepaard uitvoert. Overigens kun je deze (within) vergelijking wel door spss laten doen. Namelijk door onder 'Options' de factor 'tijd' naar 'Display means for' te brengen en dan 'compare main effects' aan te klikken, met gewenste correctiemethode.

Op deze site van David Howell staan zeer veel adviezen over de zin en onzin van post hoc tests bij repeated measurements ANOVA's.

Waar vind ik de repeated measurements ANOVA in SPSS?

Je vindt de repeated measurements ANOVA in SPSS 16 onder Analyze->General Linear Model->Repeated measures.

Er geldt voor de repeated measurements ANOVA dat de herhaalde metingen van de patienten in aparte kolommen naast elkaar in de SPSS file moeten staan. Stel dat er drie herhaalde metingen van drie patienten zijn, dan ziet de data file er als volgt uit met vier kolommen:

patientnummer	meting1	meting2	meting3
1	10	9	11
2	8	11	12
3	5	8	9

Hoe kan ik data van 4 experimenten combineren?

De experimenten die ik verricht, heb ik in 4 sessies opgesplitst, aangezien het niet behapbaar was alle samples in een keer te verwerken. Nu blijkt dat de vergelijkingsgroepen (verschillende diagnoses) binnen elke serie toch wel erg klein zijn en vraag ik me af of en hoe ik de data van de 4 series zou kunnen combineren.

Wat wel gebruikt wordt bij zulk soort settings is het toepassen van een factor correctie. Zie ook de 4e referentie op deze pagina. Je kunt ook binnen een statistisch model een correctie voor de 'clustering' binnen sessies meenemen, bijvoorbeeld door een mixed of glm-repeated analyse te doen. Je beschouwt de experimenten dan als 'herhaalde metingen' binnen een sessie.

Referenties

• Statnotes GLM Repeated measures - zeer uitgebreide uitleg over de SPSS specificatie van een repeated measures ANOVA (engelstalig)
• Statnotes Mixed Models - zeer uitgebreide uitleg over mixed models en uitgebreide behandeling van wanneer voor mixed en wanneer voor GLM te kiezen (engelstalig)
• Move Over ANOVA: Progress in Analyzing Repeated-Measures Data and Its Reflection in Papers Published in the Archives of General Psychiatry. Gueorguieva R, Krystal JH. Arch Gen Psychiatry. 2004 Mar;61(3):310-7.
• Ruijter JM, Thygesen HH, Schoneveld OJ, Das AT, Berkhout B, Lamers WH, Factor correction as a tool to eliminate between-session variation in replicate experiments: application to molecular biology and retrovirology, Retrovirology. 2006 Jan 6;3:2
• GEE newsletter van Cornell Statistical Consulting Unit, Cornell University.
• West BT, Analyzing Longitudinal Data With the Linear Mixed Models Procedure in SPSS. Eval Health Prof 2009 32: 207-228
• The analysis factor info over het onderscheid tussen de repeated en de random statement in SPSS mixed.
• The analysis factor info over de verschillende aanpakken voor herhaalde metingen: repeated measurements anova, marginal model, mixed model.

Sofwaretips

• GLLAMM Een familie functies (vrij te downloaden/attachen) in Stata, waarbij er opties zijn voor het modelleren van herhaaldelijk gemeten niet continue uitkomstmaten (dichotome, ordinale etc).
• SuperMix Een standalone programma geschikt voor het modelleren van herhaaldelijk gemeten niet continue uitkomstmaten (dichotome, ordinale etc).

Terug naar OVERZICHT voor een overzicht van alle statistische onderwerpen op deze wiki.

Terug naar KEUZE TOETS voor hulp bij het uitzoeken van een geschikte toets of analyse.